2319. В окружность вписан прямоугольный треугольник ABC
с гипотенузой AB
. Пусть K
— середина дуги BC
, не содержащей точки A
; N
— середина отрезка AC
; M
— точка пересечения луча KN
с окружностью. В точках A
и C
проведены касательные к окружности, которые пересекаются в точке E
. Докажите, что угол EMK
прямой.
Решение. По теореме о произведении отрезков пересекающихся хорд MN\cdot NK=AN\cdot NC
.
Пусть O
— центр окружности. Касательная перпендикулярна радиусу, проведённому в точку касания, поэтому из точек A
и C
отрезок OE
виден под прямым углом. Значит, эти точки лежат на окружности с диаметром OE
. Прямая OE
— серединный перпендикуляр к отрезку AC
, значит, OE
проходит через середину N
отрезка AC
. По теореме о произведении отрезков пересекающихся хорд AN\cdot NC=EN\cdot NO
, поэтому MN\cdot NK=EN\cdot NO
. Следовательно, точки M
, K
, E
и O
лежат на одной окружности (см. задачу 114). Вписанные в эту окружность углы EMK
и EOK
опираются на одну и ту же дугу, поэтому \angle EMK=\angle EOK
. Осталось заметить, что \angle EOK=90^{\circ}
.
Действительно, точка K
— середина дуги BC
, поэтому OK\perp BC
, а так как AC\perp BC
, то OK\parallel AC
. Значит, OK\perp OE
. Что и требовалось доказать.
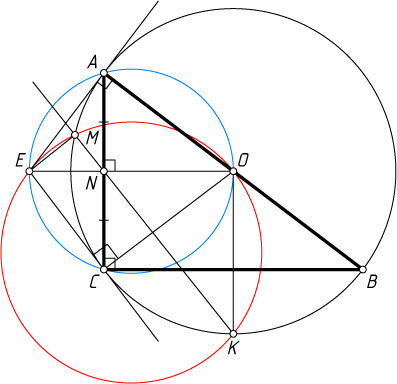
Автор: Шарыгин И. Ф.
Источник: Московская математическая олимпиада. — 2003, LXVI, 9 класс
Источник: Журнал «Квант». — 2003, № 4, с. 53
Источник: Фёдоров Р. М. и др. Московские математические олимпиады. 1993—2005 / Под ред. В. М. Тихомирова. — М.: МЦНМО, 2006. — № 5, с. 57
Источник: Турнир городов. — 2002-2003, XXIV, весенний тур, старшие классы, основной вариант
