2320. В трапеции ABCD
на боковой стороне AB
дана точка K
. Через точку A
провели прямую l
, параллельную прямой KC
, а через точку B
— прямую m
, параллельную прямой KD
. Докажите, что точка пересечения прямых l
и m
лежит на стороне CD
.
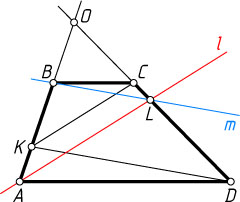
Решение. Пусть O
— точка пересечения продолжений боковых сторон AB
и CD
трапеции, L
— точка пересечения прямой l
с боковой стороной CD
. По теореме о пропорциональных отрезках \frac{OL}{OC}=\frac{OA}{OK}
и \frac{OC}{OD}=\frac{OB}{OA}
. Перемножая эти равенства, получим, что \frac{OL}{OD}=\frac{OB}{OK}
. Значит, BL\parallel KD
, а так как через точку B
проходит единственная прямая, параллельная прямой KD
, то прямая BL
совпадает с прямой m
. Отсюда следует утверждение задачи.
Автор: Бугаенко В. О.
Источник: Турнир городов. — 2001-2002, XXIII, осенний тур, младшие классы, тренировочный вариант
