2325. Между двумя параллельными прямыми расположили окружность радиуса 1, касающуюся обеих прямых, и равнобедренный треугольник, основание которого лежит на одной прямой, а вершина — на другой. Известно, что треугольник и окружность имеют ровно одну общую точку, и что эта точка лежит на вписанной окружности треугольника. Найдите радиус вписанной окружности треугольника.
Ответ. \frac{1}{2}
.
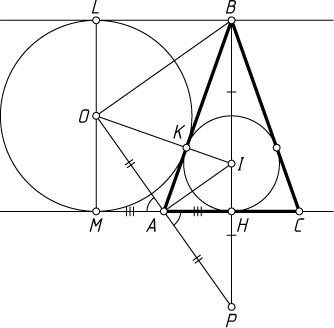
Решение. Первый способ. Пусть основание AC
равнобедренного треугольника ABC
лежит на одной из данных параллельных прямых (рис. 1), вершина B
— на другой, окружность с центром O
касается прямой AC
в точке M
, I
— центр вписанной окружности треугольника ABC
, K
— точка касания окружностей.
Линия центров касающихся окружностей проходит через точку касания, поэтому точка K
лежит на отрезке OI
.
Продолжим высоту BH
треугольника ABC
и отрезок OA
до пересечения в точке P
. Отрезки касательных, проведённых к окружности из одной точки, равны, поэтому AM=AK=AH
.
Прямоугольные треугольники AMO
и AHP
равны по катету и прилежащему острому углу, поэтому A
— середина OP
. Следовательно, BA
— медиана треугольника BOP
.
Лучи AI
и AO
— биссектрисы смежных углов CAB
и BAM
, поэтому IA\perp OP
. Лучи BO
и AO
— биссектрисы внутренних односторонних углов, поэтому BO\perp AP
. Значит, AI\parallel BO
, а так как A
— середина OP
, то I
— середина BP
. Следовательно, OI
— вторая медиана треугольника BOP
.
Поскольку медианы треугольника делятся точкой пересечения в отношении 1:2
, считая от вершины, IK=\frac{1}{2}OK=\frac{1}{2}
.
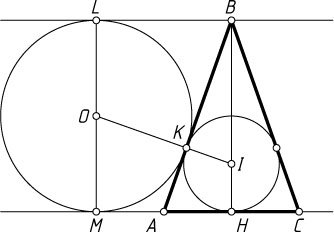
Второй способ. Пусть основание AC
равнобедренного треугольника ABC
лежит на одной из данных параллельных прямых (рис. 2), вершина B
— на другой, окружность с центром O
касается прямой AC
в точке M
, а второй из данных прямых — в точке L
, I
— центр вписанной окружности треугольника ABC
, K
— точка касания окружностей.
При гомотетии с центром K
, переводящей окружность с центром I
в окружность с центром O
, касательная AC
к первой окружности переходит в параллельную ей касательную BL
ко второй, точка I
переходит в O
, а точка A
— в B
. Значит, точка касания H
первой окружности переходит в точку касания L
второй. Следовательно, отрезок AH
переходит в отрезок BL
, равный MH
(BLMH
— прямоугольник). Значит, AH=\frac{1}{2}MH=\frac{1}{2}BL
, поэтому коэффициент гомотетии равен \frac{1}{2}
. Следовательно, IK=\frac{1}{2}OK=\frac{1}{2}
.
Автор: Гордин Р. К.
Источник: Турнир городов. — 2000-2001, XXII, осенний тур, младшие классы, основной вариант

