2326. Длины сторон треугольника ABC
равны a
, b
и c
(AB=c
, BC=a
, CA=b
и a\lt b\lt c
). На лучах BC
и AC
отмечены соответственно такие точки B_{1}
и A_{1}
, что BB_{1}=AA_{1}=c
. На лучах CA
и BA
отмечены соответственно такие точки C_{2}
и B_{2}
, что CC_{2}=BB_{2}=a
. Найдите отношение A_{1}B_{1}:C_{2}B_{2}
.
Ответ. \frac{c}{a}
Указание. \overrightarrow{A_{1}B_{1}}=\overrightarrow{A_{1}A}+\overrightarrow{AB}+\overrightarrow{BB_{1}}.
Решение. Обозначим \frac{c}{a}=\alpha
. Тогда
\overrightarrow{A_{1}B_{1}}=\overrightarrow{A_{1}A}+\overrightarrow{AB}+\overrightarrow{BB_{1}}=\alpha\overrightarrow{CC_{2}}+\alpha\overrightarrow{B_{2}B}+\alpha\overrightarrow{BC}=
=\alpha(\overrightarrow{CC_{2}}+\overrightarrow{B_{2}B}+\overrightarrow{BC})=\alpha(\overrightarrow{B_{2}B}+\overrightarrow{BC}+\overrightarrow{CC_{2}})=\alpha\overrightarrow{B_{2}C_{2}}.
Следовательно,
\frac{A_{1}B_{1}}{C_{2}B_{2}}=\alpha=\frac{c}{a}.
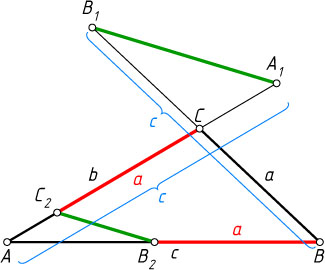
Автор: Женодаров Р. Г.
Источник: Турнир городов. — 2000-2001, XXII, осенний тур, старшие классы, основной вариант
