2329. Внутри угла с вершиной M
отмечена точка A
. Из этой точки выпустили шар, который отразился от одной стороны угла в точке B
, затем от другой стороны в точке C
и вернулся в A
(«угол падения» равен «углу отражения»). Докажите, что центр O
окружности, описанной около треугольника BCM
, лежит на прямой AM
. (Шар считайте точкой.)
Решение. Пусть P
— точка на продолжении отрезка MB
за точку B
, Q
— точка на продолжении отрезка BC
за точку B
. Тогда
\angle ABP=\angle CBM=\angle PBQ.
Следовательно, BM
— биссектриса внешнего угла при вершине B
треугольника ABC
. Аналогично CM
— биссектриса внешнего угла при вершине C
этого треугольника. Биссектрисы двух внешних и третьего внутреннего углов треугольника пересекаются в одной точке, поэтому AM
— биссектриса угла BAC
.
Перпендикуляры, восставленные из точек B
и C
к сторонам данного угла, являются биссектрисами внутренних углов при вершинах B
и C
треугольника ABC
, поэтому они пересекаются в точке I
, лежащей на биссектрисе угла при вершине A
. Из точек B
и C
отрезок MI
виден под прямым углом, значит, эти точки лежат на окружности с диаметром MI
. Эта окружность описана около треугольника BCM
, а её центр лежит на прямой AM
.
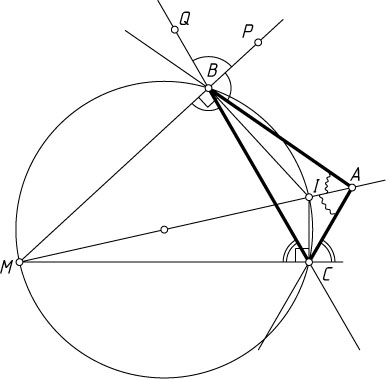
Автор: Шарыгин И. Ф.
Автор: Заславский А. А.
Источник: Турнир городов. — 2000-2001, XXII, весенний тур, младшие классы, основной вариант
