2332. Вневписанные окружности касаются сторон AC
и BC
треугольника ABC
в точках K
и L
. Докажите, что прямая, проходящая через середины отрезков KL
и AB
,
а) делит периметр треугольника ABC
пополам;
б) параллельна биссектрисе угла ACB
или содержит её.
Решение. Лемма 1. Если точки P
и Q
лежат на сторонах AC
и BC
треугольника ABC
и AP=BQ
, то прямая проходящая через середины PQ
и AB
, параллельна биссектрисе угла BAC
или содержит её.
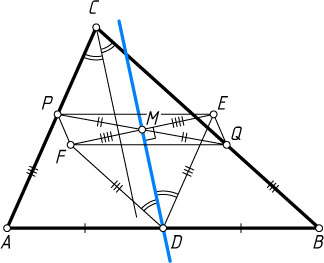
Доказательство. Пусть точки P
и Q
лежат на сторонах AC
и BC
соответственно (рис. 1), M
— середина PQ
, D
— середина AB
.
Построим параллелограммы ADEP
и BDFQ
. Поскольку PE=AD=BD=FQ
и PE\parallel AB\parallel FQ
, четырёхугольник PEQF
— также параллелограмм. Его диагональ EF
проходит через середину M
диагонали PQ
.
Поскольку DE=AP=BQ=DF
, треугольник EDF
— равнобедренный. Его медиана DM
является биссектрисой. Лучи DE
и DF
противоположно направлены лучам CA
и CB
соответственно. Следовательно, если AC\ne BC
, то прямая DM
параллельна биссектрисе угла ACB
, а если AC=BC
, то прямая DM
содержит эту биссектрису. Лемма доказана.
Лемма 2. Если K
— точка касания вневписанной окружности треугольника ABC
со стороной AC
, то AK=p-AB
, где p
— полупериметр треугольника.
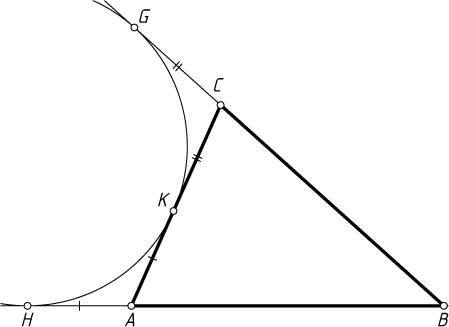
Доказательство. Пусть H
и G
— точки касания вневписанной окружности треугольника ABC
с продолжениями сторон AB
и BC
соответственно (рис. 2). Тогда
AK=AH,~CK=CG,~2p=AB+AK+CK+BC=
=(AB+AH)+(CG+BC)=BH+BG=2BH,
значит, BH=p
, Следовательно,
AK=AH=BH-AB=p-AB.
Лемма доказана.
Перейдём к нашей задаче.
б) Если AC=BC
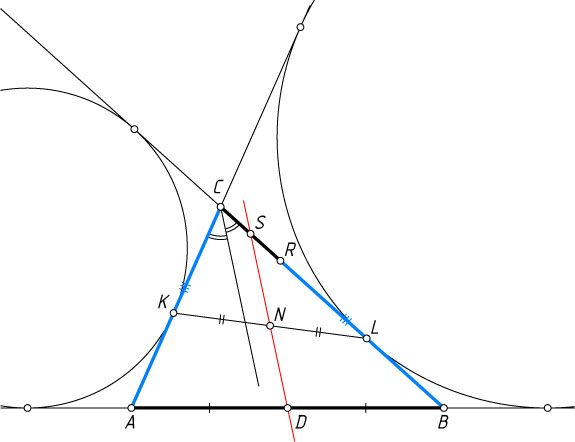
, утверждение очевидно. Предположим, что AC\ne BC
(рис. 3). Пусть N
— середина KL
. Поскольку AK=p-AB
и BL=p-AB
(по лемме 2), то AK=BL
. Следовательно, по лемме 1 прямая DN
параллельна биссектрисе угла ACB
. Что и требовалось доказать.
а) Если AC=BC
, утверждение очевидно. Предположим, что AC\lt BC
. На стороне BC
отложим отрезок BR=AC
. Пусть S
— середина отрезка CR
. Тогда
AD+AC+CS=DB+BR+RS.
Поэтому, прямая DS
делит периметр треугольника ABC
пополам, а так как по лемме 1 прямая DS
параллельна биссектрисе угла ACB
, то DS\parallel DN
. Значит, прямые DS
и DN
совпадают. Следовательно, прямая DN
делит периметр треугольника ABC
пополам. Что и требовалось доказать.
Автор: Емельянов Л. А.
Источник: Турнир городов. — 1999-2000, XXI, осенний тур, старшие классы, основной вариант
Источник: Журнал «Квант». — 2000, № 3, с. 25, М1728
Источник: Задачник «Кванта». — М1728


