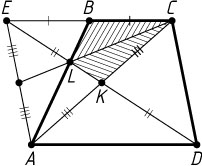
2333. В трапеции ABCD
площади 1 основания BC
и AD
относятся как 1:2
. Пусть K
— середина диагонали AC
. Прямая DK
пересекает сторону AB
в точке L
. Найдите площадь четырёхугольника BCKL
.
Ответ. \frac{2}{9}
.
Решение. Рассмотрим параллелограмм ADCE
. Его диагонали пересекаются в середине AC
, т. е. в точке K
. Поскольку CE=AD=2BC
, точка B
— середина стороны CE
треугольника ACE
, а L
— точка пересечения медиан этого треугольника.
Поскольку третья медиана треугольника ACE
проходит через точку L
, а медианы треугольника разбивают его на 6 равновеликих треугольников,
S_{BCKL}=S_{\triangle BCL}+S_{\triangle KCL}=\frac{1}{3}S_{\triangle ACE}.
Отношение площадей треугольников ACD
и ABC
равно отношению их оснований AD
и BC
, т. е. 2. Значит,
S_{\triangle ACE}=S_{\triangle ACD}=\frac{2}{3}S_{ABCD}=\frac{2}{3}.
Следовательно,
S_{BCKL}=\frac{1}{3}S_{\triangle ACE}=\frac{1}{3}\cdot\frac{2}{3}=\frac{2}{9}.
Источник: Турнир городов. — 1999-2000, XXI, весенний тур, младшие классы, тренировочный вариант
Источник: Гордин Р. К. ЕГЭ 2013. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2014. — № 2.21, с. 21
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 2.21.1, с. 21
