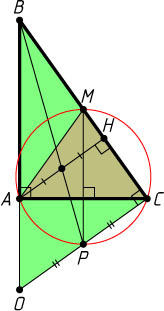
2340. В треугольнике ABC
угол A
прямой, M
— середина BC
, H
— основание высоты из вершины A
. Прямая, проходящая через точку M
перпендикулярно AC
, вторично пересекает описанную окружность треугольника AMC
в точке P
. Докажите, что отрезок BP
делит отрезок AH
пополам.
Решение. Поскольку MP
— серединный перпендикуляр к отрезку AC
, прямые AB
и MP
параллельны, а MP
— диаметр описанной окружности треугольника AMC
(серединный перпендикуляр к хорде проходит через центр окружности).
Пусть прямые AB
и CP
пересекаются в некоторой точке O
. Поскольку \angle PCM=90^{\circ}
(точка C
лежит на окружности с диаметром MP
), то OC\parallel AH
, а так как AB\perp AC
и MP\perp AC
, то MP\parallel AB
. Значит, MP
— средняя линия треугольника BCO
, а P
— середина отрезка CO
.
Следовательно, медиана BP
треугольника BCO
делит отрезок AH
, параллельный OC
, пополам. Что и требовалось доказать.
Источник: Турнир городов. — 2007-2008, XXIX, весенний тур, старшие классы, тренировочный вариант
