2342. В выпуклом четырёхугольнике ABCD
нет параллельных сторон. Углы, образованные сторонами четырёхугольника с диагональю AC
, равны (в каком-то порядке) 16^{\circ}
, 19^{\circ}
, 55^{\circ}
и 55^{\circ}
. Каким может быть острый угол между диагоналями AC
и BD
?
Ответ. 87^{\circ}
.
Решение. Пусть E
— точка пересечения диагоналей. Поскольку в четырёхугольнике нет параллельных сторон, достаточно рассмотреть два варианта расположения углов.
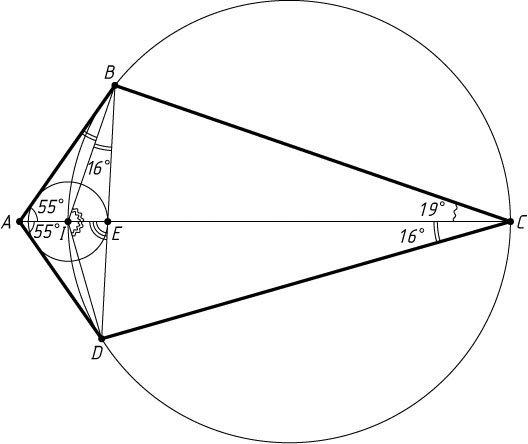
1) \angle BAC=\angle DAC=55^{\circ}
, \angle BCA=19^{\circ}
, \angle DCA=16^{\circ}
(рис. 1).
Пусть I
— точка пересечения биссектрис треугольника ABD
. Четырёхугольник BCDI
вписанный, так как
\angle BID=180^{\circ}-\angle IBE-\angle IDE=180^{\circ}-\frac{1}{2}(\angle ABE+\angle ADE)=
=180^{\circ}-\frac{1}{2}(180^{\circ}-2\cdot55^{\circ})=180^{\circ}-35^{\circ}=145^{\circ},
\angle BID+\angle BCD=145^{\circ}+35^{\circ}=180^{\circ}.
Поэтому \angle DBI=\angle DCI=\angle DCA=16^{\circ}
. Значит, \angle ABD=32^{\circ}
. Следовательно,
\angle AED=\angle ABD+\angle BAC=32^{\circ}+55^{\circ}=87^{\circ}.
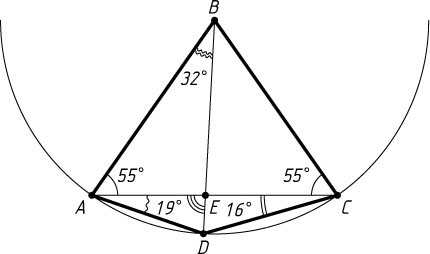
2) \angle BAC=\angle BCA=55^{\circ}
, \angle DAC=19^{\circ}
, \angle DCA=16^{\circ}
(рис. 2).
Тогда \angle ADC=145^{\circ}
, \angle ABC=70^{\circ}
.
Рассмотрим описанную окружность треугольника ADC
. Центр этой окружности является вершиной равнобедренного треугольника с основанием AC
и углом при вершине, равным 360^{\circ}-2\cdot145^{\circ}=70^{\circ}
, т. е. совпадает с точкой B
. Поэтому \angle ABD=2\angle DCA=32^{\circ}
. Следовательно,
\angle AED=\angle ABD+\angle BAC=32^{\circ}+55^{\circ}=87^{\circ}.
Источник: Турнир городов. — 2007-2008, XXIX, весенний тур, младшие классы, основной вариант

