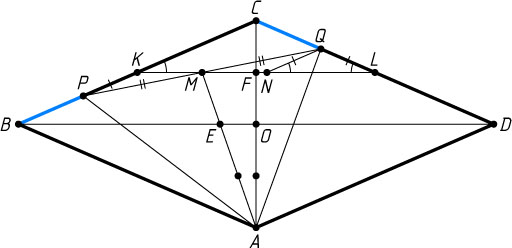
2352. На сторонах BC
и CD
ромба ABCD
взяли точки P
и Q
соответственно так, что BP=CQ
. Докажите, что точка пересечения медиан треугольника APQ
лежит на диагонали BD
ромба.
Указание. Достаточно доказать, что середина отрезка PQ
лежит на прямой, параллельной BD
и расположенной в 1,5 раза дальше от A
, чем BD
.
Решение. Пусть K
и L
— середины сторон BC
и CD
соответственно. Докажем, что середина отрезка PQ
лежит на средней линии KL
треугольника BCD
.
Предположим, что точка Q
лежит между C
и L
. Через точку Q
проведём прямую, параллельную BC
. Пусть N
— точка её пересечения с прямой KL
, а M
— точка пересечения KL
и PQ
. Треугольник NQL
равнобедренный, поэтому
QN=QL=CL-CQ=BK-BP=PK.
Значит, треугольники QMN
и PKM
равны по стороне и двум прилежащим к ней углам. Следовательно, QM=PM
, т. е. M
— середина отрезка PQ
. Что и требовалось доказать. Аналогично для случая, когда точка Q
лежит между D
и L
. Таким образом, AM
— медиана треугольника APQ
.
Пусть диагональ BD
ромба пересекает отрезок AM
в точке E
, а диагональ AC
пересекает отрезок KL
в точке F
. Средняя линия KL
треугольника BCD
делит диагональ AC
в отношении \frac{AF}{FC}=3
, а центр O
ромба делит эту диагональ пополам, поэтому O
делит отрезок AF
в отношении \frac{AO}{OF}=2
. Поскольку OE\parallel KL
, точка E
делит в том же отношении медиану AM
треугольника APQ
. Таким образом, точка E
, лежащая на медиане AM
треугольника APQ
, делит эту медиану в отношении 2:1
, считая от вершины A
. Следовательно, точка E
, лежащая на диагонали BD
, — точка пересечения медиан треугольника APQ
. Что и требовалось доказать.
Автор: Произволов В. В.
Источник: Турнир городов. — 2009-2010, XXXI, осенний тур, младшие классы, основной вариант
Источник: Журнал «Квант». — 2009, № 5, с. 29
