2360. Дана равнобокая трапеция ABCD
(AD\parallel BC
). На дуге AD
(не содержащей точек B
и C
) описанной окружности этой трапеции произвольно выбрана точка M
. Докажите, что основания перпендикуляров, опущенных из вершин A
и D
на отрезки BM
и CM
, лежат на одной окружности.
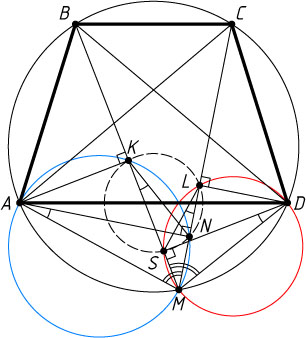
Решение. Рассмотрим случай, изображённый на рисунке. Из точек K
и N
отрезок AM
виден под прямым углом, значит, эти точки лежат на окружности с диаметром AM
. Вписанные в эту окружность углы MKN
и MAN
опираются на одну и ту же дугу, поэтому
\angle SKN=\angle MKN=\angle MAN=90^{\circ}-\angle AMN=90^{\circ}-\angle AMC.
Аналогично
\angle SLN=\angle SLM=\angle SDM=90^{\circ}-\angle SMD=90^{\circ}-\angle BMD.
Рассмотрим описанную окружность данной трапеции. Вписанные углы AMC
и BMD
опираются на равные дуги ABC
и BCD
, поэтому \angle AMC=\angle BMD
. Значит,
\angle SKN=90^{\circ}-\angle AMC=90^{\circ}-\angle BMD=\angle SLN.
Из точек K
и L
, лежащих по одну сторону от прямой NS
, отрезок NS
виден под одним и тем же углом, следовательно, точки K
, L
, N
и S
лежат на одной окружности. Что и требовалось доказать.
Аналогично для всех остальных случаев.
Источник: Всероссийская олимпиада школьников. — 2012-2013, окружной тур, 10 класс
