2361. Точка X
расположена на диаметре AB
окружности радиуса R
. Точки K
и N
лежат на окружности в одной полуплоскости относительно AB
, а \angle KXA=\angle NXB=60^{\circ}
. Найдите длину отрезка KN
.
Ответ. R
.
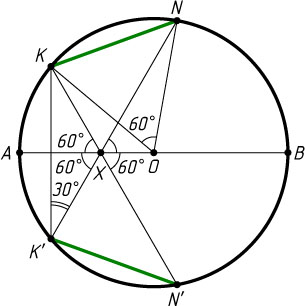
Решение. Первый способ. При симметрии относительно диаметра AB
окружность переходит в себя, точка K
— в точку K'
, лежащую на окружности, а луч XK
— в луч XK'
, причём \angle K'XA=\angle KXA=\angle NXB
. Значит, точки N
, X
и K'
лежат на одной прямой.
В равнобедренном треугольнике KXK'
угол при вершине X
равен 2\cdot60^{\circ}=120^{\circ}
, значит \angle NK'K=30^{\circ}
.
В то же время, центральный угол KON
вдвое больше вписанного угла KK'N
, значит, \angle KON=60^{\circ}
, а так как треугольник KON
равнобедренный, то он равносторонний. Следовательно, KN=OK=R
.
Второй способ. Лемма. Если точки X
и O
лежат на прямой a
, лучи XK
и XN
образуют с этой прямой равные углы, а точка O
равноудалена от K
и N
, то точки K
, N
, X
и O
лежат на одной окружности.
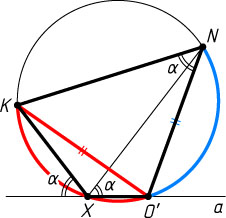
Доказательство. Пусть лучи XK
и XN
образуют с прямой a
углы, равные \alpha
, а окружность, описанная около треугольника KNX
, пересекает прямую a
в точке O'
. Четырёхугольник KNO'X
— вписанный, поэтому
\angle KNO'=180^{\circ}-\angle KXO'=\alpha.
В то же время, вписанные углы NKO'
и NXO'
опираются на одну и ту же дугу, поэтому \angle NKO'=\angle NXO'=\alpha
. Значит, треугольник NKO'
равнобедренный. Таким образом, точки O
и O'
лежат и на серединном перпендикуляре к отрезку KN
, и на прямой a
. Значит, эти точки совпадают. Следовательно, точки K
, N
, X
и O
лежат на одной окружности. Лемма доказана.
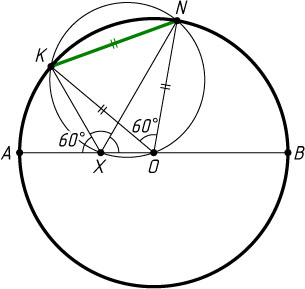
Переходим к нашей задаче. По доказанной лемме точки K
, N
, X
и центр O
данной окружности лежат на одной окружности. Тогда \angle KON=\angle KXN=60^{\circ}
, значит, равнобедренный треугольник KON
— равносторонний. Следовательно, KN=OK=R
.
Источник: Всероссийская олимпиада школьников. — 2012-2013, окружной тур, 11 класс


