2364. Две окружности пересекаются в точках E
и F
. Прямая l
пересекает первую окружность в точках A
и B
, вторую — в точках C
и D
так, что точка E
лежит внутри треугольника ADF
, а точки B
и C
— на отрезке AD
. Оказалось, что AB=CD
. Докажите, что BE\cdot DF=CE\cdot AF
.
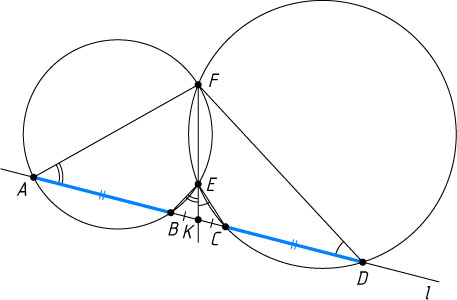
Указание. Прямая FE
пересекает отрезок BC
в его середине.
Решение. Пусть продолжение общей хорды FE
окружностей пересекает отрезок BC
в точке K
. Обозначим AB=CD=x
. Тогда BK\cdot KA=KE\cdot KF=CK\cdot KD
, поэтому
BK\cdot KA=CK\cdot KD~\Leftrightarrow~BK(BK+x)=CK(CK+x)~\Leftrightarrow
\Leftrightarrow~BK^{2}-CK^{2}+x(BK-CK)=0~\Leftrightarrow
\Leftrightarrow~(BK-CK)(BK+CK+x)=0,
значит, BK=CK
. Следовательно, K
— середина отрезка BC
.
Сумма противоположных углов вписанного четырёхугольника равна 180^{\circ}
, поэтому
\angle CDF=180^{\circ}-\angle CEF=\angle CEK.
Тогда треугольники KCE
и KFD
подобны по двум углам, значит, \frac{CE}{DF}=\frac{CK}{KF}
. Аналогично \frac{BE}{AF}=\frac{BK}{KF}
, а так как CK=BK
, то \frac{CE}{DF}=\frac{BE}{AF}
. Следовательно, BE\cdot DF=CE\cdot AF
. Что и требовалось доказать.
Автор: Максимов Д.
Источник: Санкт-Петербургская (Ленинградская) математическая олимпиада. — 2011, первый тур, 10 класс
