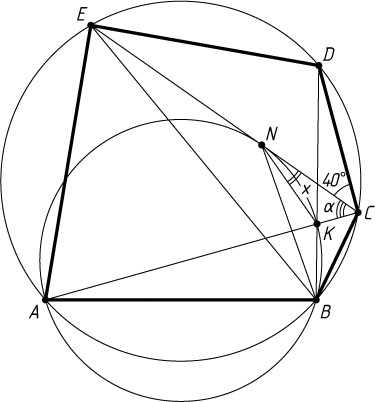
2365. В окружность вписан пятиугольник ABCDE
. Отрезки AC
и BD
пересекаются в точке K
. Отрезок CE
касается описанной окружности треугольника ABK
в точке N
. Найдите угол CNK
, если известно, что \angle ECD=40^{\circ}
.
Ответ. 20^{\circ}
.
Решение. Обозначим \angle CNK=x
, \angle ACE=\alpha
. Из теоремы об угле между касательной и хордой следует, что
\angle KBN=\angle CNK=x,
а из теоремы о вписанных углах, опирающихся на одну и ту же дугу, —
\angle ABE=\angle ACE=\alpha.
По теореме о внешнем угле треугольника
\angle AKN=\angle CNK+\angle ACE=x+\alpha.
Тогда
\angle ABN=\angle AKN=x+\alpha,
значит,
\angle NBE=\angle ABN-\angle ABE=x+\alpha-\alpha=x.
Поэтому
\angle DBE=\angle NBE+\angle KBN=x+x=2x.
В то же время, вписанные углы DBE
и ECD
опираются на одну и ту же дугу, значит,
2x=\angle DBE=\angle ECD=40^{\circ}.
Следовательно, \angle CNK=x=20^{\circ}
.
Автор: Смирнов А. В.
Источник: Санкт-Петербургская (Ленинградская) математическая олимпиада. — 2011, первый тур, 11 класс
