2366. Внутри треугольника даны точки A
, B
, C
и D
. Докажите, что на сторонах треугольника найдётся такая точка K
, что KA+KB\geqslant KC+KD
.
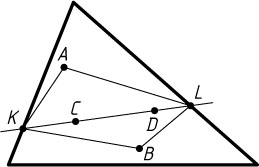
Решение. Пусть прямая CD
пересекает стороны треугольника в точках K
и L
. Докажем, что для одной из этих точек верно нужное неравенство.
Предположим, что это не так, т. е. KA+KB\lt KC+KD
и LA+LB\lt LC+LD
. Сложив эти неравенства, получим, что
KA+KB+LA+LB\lt KC+KD+LC+LD=
=(KC+LC)+(KD+LD)=KL+KL=2KL.
В то же время, KA+LA\geqslant KL
и KB+LB\geqslant KL
, поэтому
KA+KB+LA+LB=(KA+LA)+(KB+LB)\geqslant KL+KL=2KL.
Получено противоречие. Следовательно, либо KA+KB\geqslant KC+KD
, либо LA+LB\geqslant LC+LD
. Что и требовалось доказать.
Автор: Берлов С. Л.
Источник: Санкт-Петербургская (Ленинградская) математическая олимпиада. — 2011, второй тур, 7 класс
