2367. На сторонах AB
, BC
и CD
выпуклого четырёхугольника ABCD
отмечены точки K
, L
и M
соответственно, причём \frac{DM}{MC}=\frac{CL}{LB}=2
и \frac{AK}{KB}=5
. Оказалось, что AB\perp LK
и DC\perp LM
. Докажите, что AC=BD
.
Указание. Отметьте середины отрезков AB
и DM
.
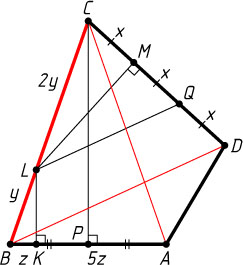
Решение. Положим
DM=2x,~MC=x,~CL=2y,~LB=y,~AK=5z,~KB=z.
Пусть P
и Q
— середины отрезков AB
и DM
соответственно. Тогда
BP=\frac{1}{2}AB=3z,~DQ=\frac{1}{2}DM=x,~CQ=2x.
Значит,
\frac{BK}{BP}=\frac{z}{3z}=\frac{1}{3}=\frac{LB}{BC},~\frac{CQ}{CD}=\frac{2x}{3x}=\frac{2}{3}=\frac{CL}{BC}.
Следовательно, KL\parallel CP
и QL\parallel BD
.
Поскольку CP\parallel KL
и KL\perp AB
, то CP\perp AB
, поэтому в треугольнике ACB
медиана CP
является высотой. Значит, треугольник ACB
равнобедренный, AC=BC
.
В треугольнике CLQ
высота LM
также является медианой, поэтому LQ=CL
, а так как треугольник CBD
подобен треугольнику CQL
с коэффициентом \frac{BC}{CL}=\frac{3}{2}
, то
BD=\frac{3}{2}LQ=\frac{3}{2}CL=\frac{3}{2}\cdot2y=3y=BC.
Таким образом, AC=BC
и BD=BC
. Следовательно, AC=BD
. Что и требовалось доказать.
Автор: Берлов С. Л.
Источник: Санкт-Петербургская (Ленинградская) математическая олимпиада. — 2011, второй тур, 8 класс
