2368. Внутри треугольника ABC
выбрана точка D
, для которой AD=DC
. Прямая BD
пересекает сторону AC
в точке E
. Оказалось, что \frac{BD}{BE}=\frac{AE}{EC}
. Докажите, что BE=BC
.
Указание. Через точку D
проведите прямую, параллельную BC
.
Решение. Через точку D
проведём прямую, параллельную BC
. Пусть она пересекает сторону AC
в точке F
. Тогда \frac{CF}{EC}=\frac{BD}{BE}=\frac{AE}{EC}
.
Поскольку AD=CD
, треугольник ADC
равнобедренный, поэтому \angle DAF=\angle DCE
.
Из равенства \frac{CF}{EC}=\frac{AE}{EC}
следует, что CF=AE
, значит, треугольники ADE
и CDF
равны по двум сторонам и углу между ними. Поэтому DF=DE
, т. е. треугольник FDE
равнобедренный. Тогда подобный ему треугольник CBE
также равнобедренный. Следовательно, BE=BC
. Что и требовалось доказать.
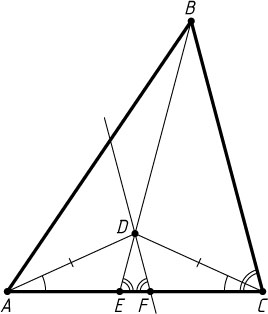
Автор: Бахарев Ф. Л.
Источник: Санкт-Петербургская (Ленинградская) математическая олимпиада. — 2011, второй тур, 9 класс
