2373. В выпуклом четырёхугольнике ABCD
точка M
— середина диагонали AC
, причём
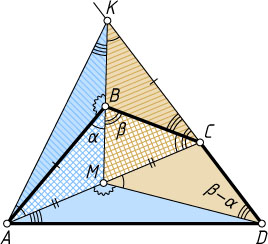
\angle MCB=\angle CMD=\angle MBA=\angle MBC-\angle MDC.
Докажите, что AD=DC+AB
.
Решение. Обозначим
\angle MCB=\angle CMD=\angle MBA=\alpha,~\angle MBC=\beta.
Тогда \angle MDC=\beta-\alpha
.
На продолжении стороны CD
за точку C
отложим отрезок CK=AB
. Тогда DC+AB=DC+CK=DK
, поэтому достаточно доказать, что DK=AD
.
Поскольку \angle MCB=\angle CMD
, прямые BC
и DM
параллельны, поэтому
\angle BCK=\angle MDC=\beta-\alpha,
\angle MCK=\angle BCM+\angle BCK=\alpha+(\beta-\alpha)=\beta.
1) Треугольники ABC
и AMB
подобны по двум углам (угол при вершине A
общий, \angle ACB=\angle ABM=\alpha
). Поэтому
\frac{MB}{BC}=\frac{AM}{AB}=\frac{MC}{CK}.
2) Отсюда следует, что треугольники MCK
и MBC
подобны по двум сторонам и углу между ними (\frac{MC}{CK}=\frac{MB}{BC}
и \angle MCK=\angle MBC=\beta
). Значит, у этих треугольников общий угол при вершине M
, т. е. точка B
лежит на отрезке MK
. Кроме того, \angle MKC=\angle MCB=\alpha
и \frac{MB}{MC}=\frac{MC}{MK}
, а так как MC=MA
, то \frac{MB}{MA}=\frac{MA}{MK}
.
3) Отсюда следует, что треугольники MBA
и MAK
подобны по двум сторонам и углу между ними (\frac{MB}{MA}=\frac{MA}{MK}
, а угол при вершине M
общий). Значит, \angle MAK=\angle MBA=\alpha
.
4) Треугольники MCD
и KBC
подобны по двум углам (\angle CMD=\angle BKC=\alpha
, \angle MDC=\angle KCB=\beta-\alpha
), поэтому \frac{MC}{MD}=\frac{KB}{KC}
. Значит,
\frac{AM}{MD}=\frac{MC}{MD}=\frac{KB}{KC}=\frac{KB}{KA}.
5) Отсюда следует, что треугольники AMD
и KBA
подобны по двум сторонам и углу между ними (\frac{AM}{MD}=\frac{KB}{KA}
, \angle AMD=180^{\circ}-\alpha=\angle KBA
). Значит, \angle AKB=\angle DAM
.
Следовательно,
\angle DKA=\angle AKB+\angle DKB=\angle DAM+\angle MAK=\angle DAK.
В треугольнике ADK
углы DKA
и DAK
равны, поэтому
AD=DK=DC+CK=DC+AB.
Что и требовалось доказать.
Автор: Акопян А. В.
Автор: Петров Ф. В.
Источник: Санкт-Петербургская (Ленинградская) математическая олимпиада. — 2011, второй тур, 11 класс
