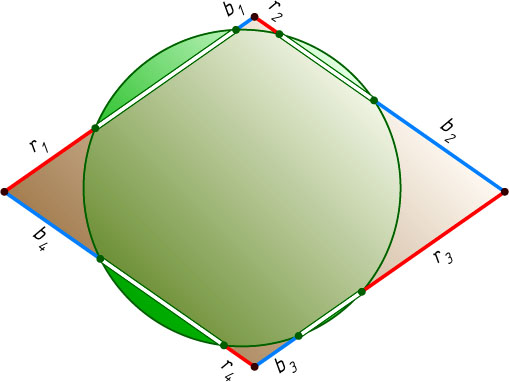
2382. Окружность пересекает каждую сторону ромба в двух точках и делит её на три отрезка. Обойдём контур ромба, начав с какой-нибудь вершины, по часовой стрелке и покрасим три отрезка каждой стороны последовательно в красный, белый и синий цвета. Докажите, что сумма красных отрезков равна сумме синих.
Указание. Произведение всей секущей на её внешнюю часть для данной окружности и данной точки постоянно
Решение. Пусть сторона ромба равна d
, а красные и синие отрезки в порядке обхода контура ромба равны r_{1}
, b_{1}
, …, r_{4}
, b_{4}
. Произведение всей секущей на её внешнюю часть для данной окружности и данной точки постоянно (степень точки относительно окружности), поэтому
r_{1}(d-b_{1})=b_{4}(d-r_{4}),~r_{2}(d-b_{2})=b_{1}(d-r_{1}),
r_{3}(d-b_{3})=b_{2}(d-r_{2}),~r_{4}(d-b_{4})=b_{3}(d-r_{3}).
Сложив эти равенства, получим, что
(r_{1}+r_{2}+r_{3}+r_{4})d-(r_{1}b_{1}+r_{2}b_{2}+r_{3}b_{3}+r_{4}b_{4})=
=(b_{1}+b_{2}+b_{3}+b_{4})d-(r_{1}b_{1}+r_{2}b_{2}+r_{3}b_{3}+r_{4}b_{4}).
Следовательно,
r_{1}+r_{2}+r_{3}+r_{4}=b_{1}+b_{2}+b_{3}+b_{4}.
Что и требовалось доказать.
Автор: Произволов В. В.
Источник: Турнир городов. — 1996-1997, XVIII, осенний тур, младшие классы, тренировочный вариант
