2391. В остроугольном треугольнике ABC
проведены высоты AA_{1}
, BB_{1}
и CC_{1}
. Точки X
и Y
— середины отрезков CA_{1}
и AC_{1}
. Известно, что XY=BB_{1}
. Докажите, что отношение каких-то двух сторон треугольника ABC
равно \sqrt{2}
.
Указание. Если M
— середина AC
, то точки X
и Y
лежат на окружности с диаметром BM
. Далее примените теорему синусов.
Решение. Пусть M
— середина стороны AC
, а X
и Y
— середины отрезков CA_{1}
и AC_{1}
соответственно. Тогда MX
и MY
— средние линии прямоугольных треугольников AA_{1}C
и AC_{1}C
, поэтому \angle BXM=\angle BYM=90^{\circ}
.
Из точек X
, Y
и B_{1}
отрезок BM
виден под прямым углом, значит, эти точки лежат на окружности с диаметром BM
. По теореме синусов
\sin\angle ABC=\frac{XY}{BM}=\frac{BB_{1}}{BM}=\sin\angle AMB,
поэтому либо \angle AMB=\angle ABC
, либо \angle CMB=\angle ABC
.
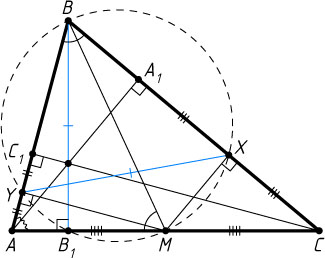
В первом случае (рис. 1) треугольник AMB
подобен треугольнику ABC
по двум углам, поэтому
\frac{AB}{AC}=\frac{AM}{AB}=\frac{\frac{1}{2}AC}{AB}=\frac{AC}{2AB}.
Следовательно, \frac{AC}{AB}=\sqrt{2}
.
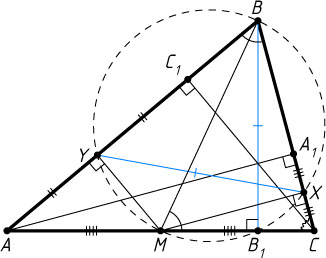
Во втором случае (рис. 2) аналогично получим, что \frac{AC}{BC}=\sqrt{2}
.
Автор: Берлов С. Л.
Источник: Санкт-Петербургская (Ленинградская) математическая олимпиада. — 2009, второй тур, 9 класс

