2392. В выпуклом четырёхугольнике ABCD
выполнено равенство AB=CD
. Его диагонали пересекаются в точке O
. Точки X
, Y
, Z
и T
— середины отрезков BC
, AD
, AC
и BD
соответственно. Докажите, что центр окружности, описанной около треугольника OZT
, лежит на прямой XY
.
Указание. Четырёхугольник ZXTY
— ромб.
Решение. Отрезок XZ
— средняя линия треугольника ABC
, поэтому XZ\parallel AB
и XZ=\frac{1}{2}AB
. Аналогично XT\parallel CD
и XT=\frac{1}{2}CD
. Значит, четырёхугольник ZXTY
— параллелограмм, а так как AB=CD
, то XZ=XT
, поэтому ZXTY
— ромб. Его диагональ XY
перпендикулярна диагонали ZT
и делит её пополам, значит, прямая XY
— серединный перпендикуляр к отрезку ZT
.
Центр Q
окружности, описанной около треугольника OZT
, равноудалён от концов отрезка ZT
, следовательно, точка Q
лежит на серединном перпендикуляре к отрезку ZT
, т. е. на прямой XY
. Что и требовалось доказать.
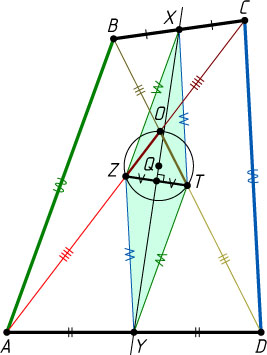
Автор: Смирнов А. В.
Источник: Санкт-Петербургская (Ленинградская) математическая олимпиада. — 2009, второй тур, 10 класс
