2393. Диагонали вписанного четырёхугольника ABCD
пересекаются в точке E
, а прямые AD
и BC
— в точке F
. Точки X
и Y
— середины сторон AD
и BC
соответственно. Точка O
— центр описанной окружности четырёхугольника ABCD
, а точка O_{1}
— центр описанной окружности треугольника EXY
. Докажите, что OF\parallel O_{1}E
.
Решение. Лемма 1. Если O_{1}
— центр описанной окружности треугольника XEY
, а EH
— высота этого треугольника, то прямые EO_{1}
и EH
симметричны относительно биссектрисы угла XEY
.
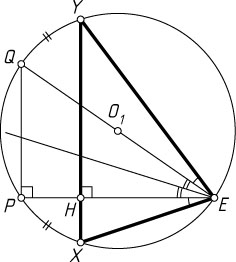
Доказательство. Рассмотрим случай, изображённый на рис. 1. Пусть высота EH
вторично пересекает описанную окружность треугольника XEY
в точке P
, а EQ
— диаметр окружности. Тогда \angle EPQ=90^{\circ}=\angle EHY
, значит, PQ\parallel XY
. Дуги, заключённые между параллельными хордами, равны, значит, \angle XEP=\angle YEQ
. Поэтому биссектриса угла XEY
является также биссектрисой угла HEO_{1}
. Следовательно, прямые EO_{1}
и EH
симметричны относительно этой биссектрисы. Аналогично для любого другого случая. Лемма доказана.
Лемма 2. Если два противоположных угла выпуклого четырёхугольника равны, то биссектрисы двух других углов параллельны или лежат на одной прямой.
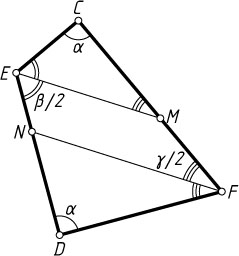
Доказательство. Пусть углы при противоположных вершинах C
и D
выпуклого четырёхугольника CFDE
равны \alpha
, а углы при вершинах E
и F
равны \beta
и \gamma
соответственно (рис. 2). Тогда 2\alpha+\beta+\gamma=360^{\circ}
, поэтому 180^{\circ}-\alpha-\frac{\beta}{2}=\frac{\gamma}{2}
.
Пусть биссектриса угла E
пересекает прямую CF
в точке M
, а биссектриса угла F
пересекает прямую DE
в точке N
. Тогда
\angle CME=180^{\circ}-\angle MCE-\angle CEM=180^{\circ}-\alpha-\frac{\beta}{2}=\frac{\gamma}{2}=\angle CFN.
Следовательно, прямые EM
и FN
параллельны или совпадают. Лемма доказана.
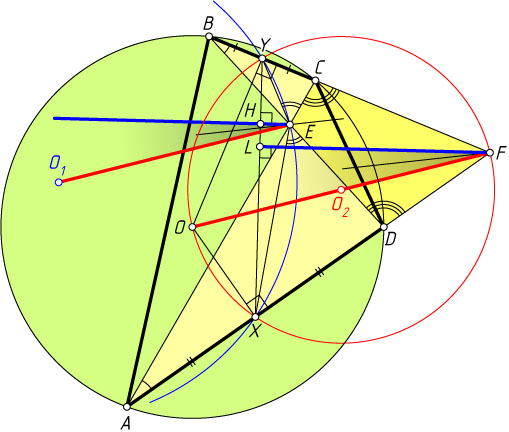
Перейдём к нашей задаче (рис. 3). Треугольники AED
и BEC
подобны по двум углам, значит, угол между медианой EX
и стороной ED
в первом треугольнике равен углу между соответствующими медианой EY
и стороной EC
во втором, т. е. \angle DEX=\angle CEY
. Тогда биссектрисы углов CED
и XEY
лежат на одной прямой.
Поскольку OX\perp AD
и OY\perp BC
, из точек X
и Y
отрезок OF
виден под прямым углом, значит, эти точки лежат на окружности с центром O_{2}
— середине FO
.
По лемме 1 при симметрии относительно биссектрисы угла XEY
прямая EO_{1}
переходит в прямую EH
, перпендикулярную XY
. Аналогично прямая FO_{2}
при симметрии относительно биссектрисы угла CFD
переходит в прямую FL
, также перпендикулярную XY
. Значит, прямые EH
и FL
параллельны.
В треугольниках FAC
и FBD
угол при вершине F
общий, а \angle FAC=\angle DAC=\angle DBC=\angle DBF
, поэтому \angle ACF=\angle BDF
.
Противоположные углы при вершинах C
и D
выпуклого четырёхугольника CFDE
равны. По лемме 2, биссектрисы углов CED
(а значит, и XEY
) и CFD
параллельны или лежат на одной прямой. Прямая EH
, симметричная прямой O_{1}E
относительно биссектрисы угла XEY
, и прямая FL
, симметричная OF
относительно биссектрисы угла CFD
, параллельны. В то же время, указанные биссектрисы параллельны или лежат на одной прямой. Следовательно, прямые O_{1}E
и OF
также параллельны. Что и требовалось доказать.
Автор: Смирнов А. В.
Источник: Санкт-Петербургская (Ленинградская) математическая олимпиада. — 2009, второй тур, 11 класс


