2396. Если окружность разделить на десять равных частей, а затем соединить соседние точки деления хордами, то получится правильный десятиугольник. Соединив хордами каждую точку деления через две точки с третьей, получим равносторонний звёздчатый десятиугольник. Докажите, что разность между длинами сторон этих двух десятиугольников равна радиусу данного круга.
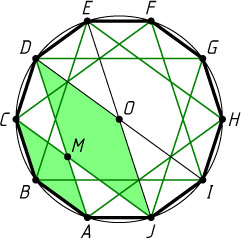
Решение. Пусть ABCDEFHGIJ
— правильный десятиугольник, вписанный в окружность радиуса R
. Диаметры ID
и JE
соответственно параллельны сторонам AB
и BC
правильного десятиугольника и сторонам JC
и AD
звёздчатого десятиугольника.
Пусть хорды AD
и JC
пересекаются в точке M
, а диаметры ID
и JE
— в точке O
. Тогда четырёхугольники ABCM
и JMDO
— ромбы. Следовательно,
AD-BC=AD-AM=MD=JO=R.
Что и требовалось доказать.
Источник: Тригг Ч. Задачи с изюминкой. — М.: Мир, 1975. — № 100, с. 31
Источник: Всесибирская физико-математическая олимпиада. — 2018-2019, первый этап, задача 4, 9 класс
