2442. Два колеса радиусов r
и R
катаются по прямой m
. Найдите геометрическое место точек пересечения M
их общих внутренних касательных.
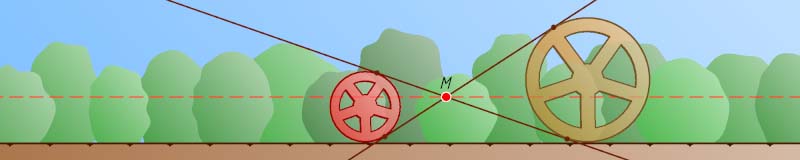
Ответ. Прямая, параллельная прямой m
.
Указание. Вычислите расстояние от точки M
до прямой m
.
Решение. Пусть O_{1}
и O_{2}
— центры окружностей радиусов r
и R
(r\lt R
), A
и B
— точки касания этих окружностей с прямой m
, C
и D
— точки касания с общей внутренней касательной.
Точка M
пересечения общих внутренних касательных к этим окружностям расположена на прямой O_{1}O_{2}
. Из подобия треугольников MO_{1}C
и MO_{2}D
следует, что
\frac{O_{1}M}{O_{2}M}=\frac{O_{1}C}{O_{2}D}=\frac{r}{R}.
Если P
— проекция точки O_{1}
на прямую O_{2}B
, то
O_{2}P=O_{2}B-BP=O_{2}B-O_{1}A=R-r.
Через точку M
проведём прямую, перпендикулярную прямой m
. Пусть Q
и D
— её точки пересечения с прямыми O_{1}P
и m
. Тогда
MD=MQ+QD=\frac{R-r}{R+r}+r=\frac{2rR}{R+r}
(треугольник O_{1}MQ
подобен треугольнику O_{1}O_{2}P
с коэффициентом \frac{O_{1}M}{O_{1}O_{2}}=\frac{r}{R+r}
). Следовательно, точка M
удалена от прямой m
на фиксированное расстояние, т. е. принадлежит прямой, параллельной прямой m
.
С другой стороны, для любой точки этой прямой можно указать две окружности радиусов r
и R
, для которых она является точкой пересечения общих внутренних касательных.
Источник: Прасолов В. В. Задачи по планиметрии. — Ч. 1. — М.: Наука, 1991. — № 7.1, с. 185
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 7.1, с. 183
Источник: Васильев Н. Б., Гутенмахер В. Л. Прямые и кривые. — 2-е изд. — М.: Наука, 1978. — № 1.2, с. 13
