2445. На плоскости даны точки A
и B
. Найдите геометрическое место точек M
, для которых разность квадратов длин отрезков AM
и BM
постоянна.
Ответ. Прямая, перпендикулярная AB
.
Указание. Воспользуйтесь теоремой Пифагора или введите прямоугольную систему координат.
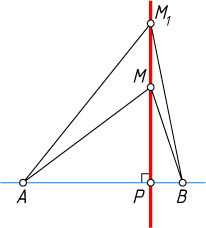
Решение. Первый способ. Пусть P
— проекция точки M
на прямую AB
и AM\gt BM
. Тогда по теореме Пифагора
AM^{2}-AP^{2}=BM^{2}-BP^{2}=MP^{2}.
Следовательно,
AM^{2}-BM^{2}=AP^{2}-BP^{2}.
Ясно, что если M_{1}
— любая точка прямой MP
, то
AM^{2}_{1}-BM^{2}_{1}=AP^{2}-BP^{2}=AM^{2}-BM^{2}.
Таким образом, достаточно на прямой AB
найти точку P
такую, что разность AP^{2}-BP^{2}
равна заданной величине. Тогда искомое геометрическое место точек есть прямая, проходящая через точку P
перпендикулярно данной прямой AB
.
Второй способ. Пусть A
и B
— данные точки и AB=c
, M
— точка, для которой MB^{2}-MA^{2}=d
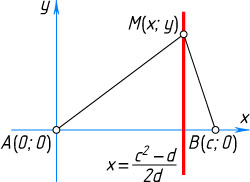
— данное число. Выберем на плоскости прямоугольную систему координат следующим образом. Начало координат — точка A
, ось абсцисс направлена по лучу AB
, ось ординат перпендикулярна AB
. Выпишем координаты данных точек: A(0;0)
и B(c;0)
.
Для того, чтобы точка M(x;y)
принадлежала искомому геометрическому месту точек, необходимо и достаточно, чтобы
MB^{2}-MA^{2}=d,~\mbox{или}~(x-c)^{2}+y^{2}-x^{2}-y^{2}=d.
После упрощения получим уравнение x=\frac{c^{2}-d}{2c}
, т. е. уравнение прямой, перпендикулярной AB
.
Источник: Петерсен Ю. Методы и теории для решения геометрических задач на построение, приложенные более чем к 400 задачам. — М.: Типография Э. Лисснера и Ю. Романа, 1892. — с. 8
Источник: Адамар Ж. Элементарная геометрия. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1948. — с. 124
Источник: Моденов П. С. Сборник задач по специальному курсу элементарной математики. — М.: Советская наука, 1957. — № 3, с. 205
Источник: Делоне Б. Н., Житомирский О. К. Задачник по геометрии. — М.—Л.: ОГИЗ, 1949. — № 232, с. 23
Источник: Прасолов В. В. Задачи по планиметрии. — Ч. 1. — М.: Наука, 1991. — № 7.6, с. 185
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 7.6, с. 184
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 298, с. 35

