2446. Стороны AB
и CD
выпуклого четырёхугольника ABCD
площади S
не параллельны. Найдите геометрическое место точек X
, лежащих внутри четырёхугольника, для которых S_{\triangle ABX}+S_{\triangle CDX}=\frac{S}{2}
.
Ответ. Отрезок.
Указание. Продолжите стороны AB
и CD
до пересечения в точке O
и отложите на лучах OA
и OB
отрезки, равные AB
и CD
.
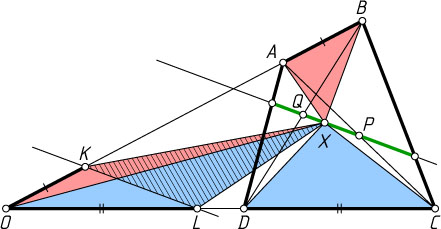
Решение. Пусть O
— точка пересечения прямых AB
и CD
. Отложим на лучах OA
и OD
отрезки OK
и OL
, равные AB
и CD
соответственно. Тогда
S_{\triangle ABX}+S_{\triangle CDX}=S_{\triangle KOX}+S_{\triangle LOX}=S_{\triangle KOL}\pm S_{\triangle KXL}.
Следовательно, площадь треугольника KXL
постоянна, т. е. точка X
лежит на прямой, параллельной KL
.
Заметим, что если P
— середина AC
, Q
— середина BD
, то
S_{\triangle ABP}+S_{\triangle CDP}=\frac{1}{2}S_{\triangle ABC}+\frac{1}{2}S_{\triangle CDA}=\frac{1}{2}S,
S_{\triangle ABQ}+S_{\triangle CDQ}=\frac{1}{2}S_{\triangle ABD}+\frac{1}{2}S_{\triangle CDB}=\frac{1}{2}S.
Значит, точки P
и Q
принадлежат искомому множеству. А поскольку доказано, что это множество — отрезок, то искомое ГМТ является отрезком (заключённым внутри ABCD
) прямой, проходящей через середины P
и Q
диагоналей AC
и BD
.
Источник: Журнал «Crux Mathematicorum». — 1977, № 3, с. 75
Источник: Прасолов В. В. Задачи по планиметрии. — Ч. 1. — М.: Наука, 1991. — № 7.2, с. 185
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 7.2, с. 184
