2453. Точки A
, B
и C
лежат на одной прямой (точка B
расположена между точками A
и C
). Через точки A
и B
проводятся окружности, а через точку C
— касательные к ним. Найдите геометрическое место точек касания.
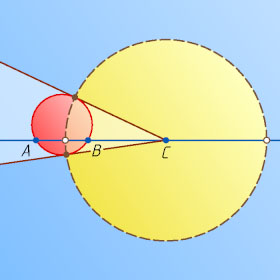
Ответ. Окружность без двух точек.
Указание. Примените теорему о касательной и секущей.
Решение. Если M
— одна из точек касания, то
CM^{2}=CA\cdot CB.
Следовательно, точка M
лежит на окружности с центром C
и радиусом, равным \sqrt{CA\cdot CB}
.
Рассмотрим теперь любую точку P
этой окружности, не лежащую на прямой AC
. Опишем окружность около треугольника APB
. Тогда треугольники APC
и PBC
подобны, поскольку угол C
у них общий, а \frac{AC}{PC}=\frac{PC}{BC}
, так как PC=\sqrt{AC\cdot BC}
. Поэтому
\angle CPB=\angle PAC=\angle PAB.
Если касательная, проведённая к описанной окружности треугольника APB
в точке P
, пересекает луч BC
в точке C_{1}
, то
\angle C_{1}PB=\angle PAB=\angle CPB.
Поэтому точки C_{1}
и C
совпадают. Следовательно, CP
— касательная к окружности, проходящей через точки A
и B
.
Источник: Пособие по математике для поступающих в вузы / Под ред. Г. Н. Яковлева. — 3-е изд. — М.: Наука, 1988. — № 4, с. 430
