2455. На сторонах AB
и BC
параллелограмма ABCD
выбраны точки A_{1}
и C_{1}
соответственно. Отрезки AC_{1}
и CA_{1}
пересекаются в точке P
. Описанные окружности треугольников AA_{1}P
и CC_{1}P
вторично пересекаются в точке Q
, лежащей внутри треугольника ACD
. Докажите, что \angle PDA=\angle QBA
.
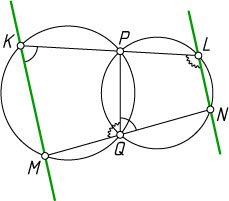
Решение. Лемма. Две окружности пересекаются в точках P
и Q
. Продолжения хорд PK
и QM
первой окружности пересекают вторую окружность в точках L
и N
соответственно. Докажите, что прямые LN
и KM
параллельны.
Доказательство. Пусть отрезки KL
и MN
не пересекаются (рис. 1). Соединим точки P
и Q
. Поскольку
\angle PQM=180^{\circ}-\angle K,~\angle PQN=180^{\circ}-\angle PQM,
то \angle PQN=\angle PKM
, а так как \angle PLN=180^{\circ}-\angle PQN
, то
\angle PLN+\angle PQM=180^{\circ}.
Следовательно, LN\parallel KM
. Аналогично для случая, когда отрезки KL
и MN
пересекаются. Лемма доказана.
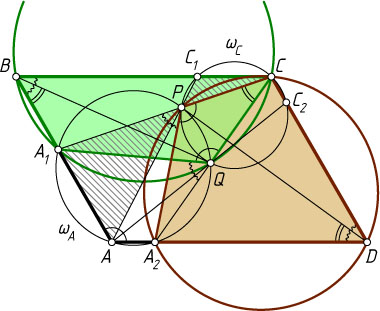
Пусть \omega_{A}
и \omega_{C}
— описанные окружности треугольников AA_{1}P
и CC_{1}P
. Применяя лемму к этим окружностям, пересекающимся в точках P
и Q
(рис. 2), получим, что точка C_{2}
пересечения прямой AQ
с \omega_{C}
лежит на стороне CD
параллелограмма ABCD
, а точка A_{2}
пересечения прямой CQ
с \omega_{A}
лежит на стороне AD
.
Четырёхугольник AA_{1}PA_{2}
вписанный, поэтому
\angle CPA_{2}=180^{\circ}-\angle A_{1}PA_{2}=\angle A_{1}AA_{2}=
=\angle BAD=180^{\circ}-\angle ADC=180^{\circ}-\angle A_{2}DC.
Значит, четырёхугольник CPA_{2}D
вписанный. Аналогично докажем, что четырёхугольник BA_{1}QC
также вписанный. Следовательно,
\angle PDA=\angle PDA_{2}=\angle PCA_{2}=\angle A_{1}CQ=\angle A_{1}BQ=\angle QBA.
Что и требовалось доказать.
Примечание. Утверждение задачи остаётся верным, если точка Q
не лежит внутри треугольника ACD
.
Автор: Емельянов Л. А.
Источник: Всероссийская олимпиада школьников. — 2008-09, XXXV, заключительный этап, 11 класс
Источник: Журнал «Квант». — 2009, № 5, с. 50

