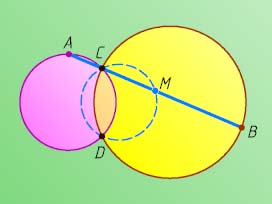
2491. Через точку пересечения двух окружностей проведена прямая, вторично пересекающая окружности в двух точках A
и B
. Найдите геометрическое место середин отрезков AB
.
Ответ. Окружность.
Указание. Пусть C
— общая точка двух данных окружностей, через которую проходит прямая AB
, а D
— вторая их общая точка. Тогда все треугольники ADB
подобны между собой.
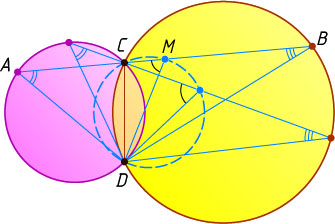
Решение. Пусть C
и D
— точки пересечения данных окружностей, M
— середина указанного отрезка AB
, проходящего через точку C
. Все треугольники ADB
подобны между собой по двум углам (например, все углы с вершиной A
равны между собой, так как они опираются на одну и ту же дугу). Значит, угол CMD
равен одному из углов между DM
и AB
(в зависимости от того, по какую сторону от CD
расположена точка M
). Следовательно, искомое геометрическое место точек есть окружность, проходящая через точки C
и D
.
Источник: Шарыгин И. Ф., Голубев В. И. Факультативный курс по математике. Решение задач: Учебное пособие для 11 кл. средней школы. — М.: Просвещение, 1991. — № 15, с. 150
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 363, с. 44

