2508. С помощью циркуля и линейки постройте окружность, касающуюся двух данных окружностей, причём одной из них — в данной точке.
Указание. Задача сводится к построению окружности, касающейся данной окружности и данной прямой в данной на ней точке.
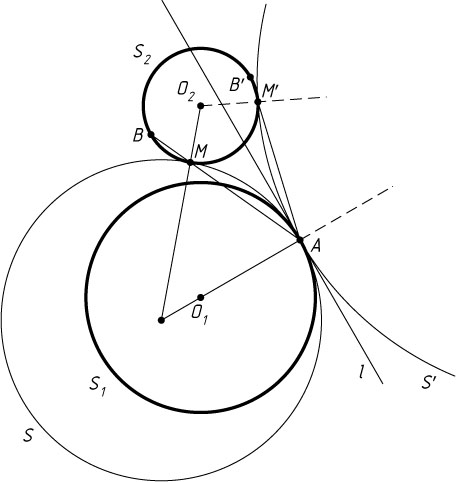
Решение. Предположим, что нужная окружность S
построена. Пусть A
— данная точка на данной окружности S_{1}
, а l
— общая касательная к окружностям S
и S_{1}
, проходящая через точку A
. Если S_{2}
— вторая данная окружность, то окружность S
касается окружности S_{2}
и прямой l
в данной на ней точке A
.
Таким образом, задача сводится к построению окружности, касающейся данной окружности (S_{2}
) и прямой (l
) в данной на ней точке (A
).
Для этого построим касательную к окружности S_{2}
, параллельную прямой l
, т. е. касательной к окружности S_{1}
, проведённой в точке A
. Ограничимся рассмотрением случая, когда данные окружности лежат по разные стороны от прямой l
. Если B
— полученная точка касания на S_{2}
, то точка M
пересечения прямой AB
с окружностью S_{2}
есть точка касания искомой окружности с окружностью S_{2}
. Если O_{1}
и O_{2}
— центры окружностей S_{1}
и S_{2}
соответственно, то пересечение прямых O_{2}M
и O_{1}A
даёт центр O
искомой окружности.
В рассматриваемом случае задача имеет два решения (внешнее и внутреннее касание окружностей S
и S_{2}
).
Источник: Петерсен Ю. Методы и теории для решения геометрических задач на построение, приложенные более чем к 400 задачам. — М.: Типография Э. Лисснера и Ю. Романа, 1892. — № 278, с. 53
