2529. Постройте треугольник ABC
, зная три точки A_{1}
, B_{1}
и C_{1}
, симметричные центру O
описанной окружности этого треугольника относительно прямых BC
, CA
и AB
.
Указание. Докажите, что O
— точка пересечения высот треугольника A_{1}B_{1}C_{1}
.
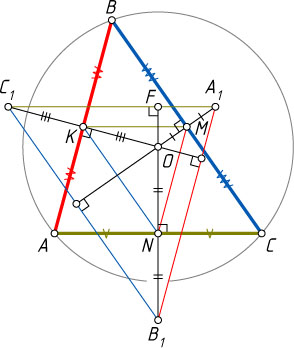
Решение. Предположим, что нужный треугольник ABC
построен. Пусть M
, N
и K
— середины его сторон BC
, CA
и AB
соответственно. Тогда MK
— средняя линия треугольников ABC
и A_{1}OC_{1}
. Поэтому MK\parallel AC
и MK\parallel A_{1}C_{1}
, а так как B_{1}O
— серединный перпендикуляр к отрезку AC
, то B_{1}O\perp A_{1}C_{1}
, т. е. высота B_{1}F
треугольника A_{1}B_{1}C_{1}
проходит через точку O
. Аналогично для остальных высот треугольника A_{1}B_{1}C_{1}
. Следовательно, O
— точка пересечения высот треугольника A_{1}B_{1}C_{1}
.
Отсюда вытекает следующий способ построения. Строим точку O
пересечения высот треугольника A_{1}B_{1}C_{1}
. Серединные перпендикуляры к отрезкам OA_{1}
, OB_{1}
и OC_{1}
есть стороны искомого треугольника ABC
.
Источник: Московская математическая олимпиада. — 1940, VI, 2-й тур, 9-10 классы
Источник: Гальперин Г. А., Толпыго А. К. Московские математические олимпиады. — М.: Просвещение, 1988. — № 16, с. 25
Источник: Куланин Е. Д., Федин С. Н. Геометрия треугольника в задачах: Экспериментальное учебное пособие для 8—10 кл. школ физико-математического направления. — М.: НИИ школ, 1990. — № 30, с. 60
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 8.30, с. 199
