2533. Даны две точки A
и B
. Найдите геометрическое место точек, каждая из которых симметрична точке A
относительно некоторой прямой, проходящей через точку B
.
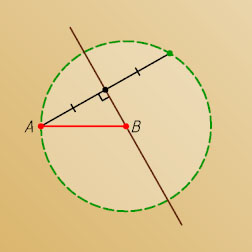
Ответ. Окружность.
Указание. На продолжении отрезка AB
за точку B
отложите отрезок BC
, равный отрезку AB
, и докажите, что отрезок AC
виден из каждой точки искомого геометрического места точек под прямым углом.
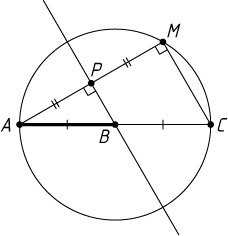
Решение. На продолжении отрезка AB
за точку B
отложим отрезок BC
, равный отрезку AB
. Докажем, что искомое геометрическое место точек есть окружность с диаметром AC
.
Пусть M
— образ точки A
при симметрии относительно некоторой прямой, проходящей через точку B
, P
— середина AM
. Тогда BP
— средняя линия треугольника AMC
. Поэтому
\angle AMC=\angle APB=90^{\circ}.
Следовательно, точка M
лежит на окружности с диаметром AC
.
Обратно, каждая точка M
этой окружности симметрична точке A
относительно прямой, проходящей через точку B
и середину отрезка AM
.
Источник: Кокстер Г. С. М. Введение в геометрию. — М.: Наука, 1966. — № 1, с. 32
Источник: Васильев Н. Б., Гутенмахер В. Л. Прямые и кривые. — 2-е изд. — М.: Наука, 1978. — № 1.10, с. 22

