2557. В выпуклом четырёхугольнике ABCD
угол ABD
равен 65^{\circ}
, угол CBD
равен 35^{\circ}
, угол ADC
равен 130^{\circ}
, и AB=BC
. Найдите углы четырёхугольника ABCD
.
Ответ. \angle BAD=57{,}5^{\circ}
, \angle BCD=72{,}5^{\circ}
.
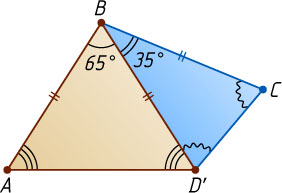
Решение. На луче BD
отложим отрезок BD'
равный AB
(рис. 1). Из равнобедренных треугольников ABD'
и BCD'
находим, что
\angle AD'B=\frac{180^{\circ}-65^{\circ}}{2}=\frac{115^{\circ}}{2},~\angle CD'B=\frac{180^{\circ}-35^{\circ}}{2}=\frac{145^{\circ}}{2},
значит,
\angle AD'C=\angle AD'B+\angle CD'B=\frac{115^{\circ}}{2}+\frac{145^{\circ}}{2}=130^{\circ}=\angle ADC.
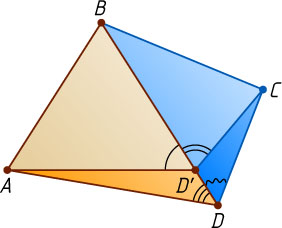
Предположим, что BD'\gt BD
(рис. 2). Тогда из теоремы о внешнем угле треугольника следует, что
\angle AD'C=\angle AD'B+\angle CD'B\lt\angle ADB+\angle CDB=\angle ADC.
Если же BD'\lt BD
, то аналогично получим, что \angle AD'C\gt\angle ADC
.
Следовательно, BD'=BD
, т. е. точка D'
совпадает с точкой D
. Тогда
\angle BAD=\angle BAD'=\angle AD'B=\frac{115^{\circ}}{2}=57{,}5^{\circ},
\angle BCD=\angle BCD'=\angle CD'B=\frac{145^{\circ}}{2}=72{,}5^{\circ}.
Источник: Санкт-Петербургская (Ленинградская) математическая олимпиада. — 1985, 8 кл.
Источник: Петербургские математические олимпиады 1961—1993 / Под ред. Д. В. Фомина, К. П. Кохася. — СПб.—М.—Краснодар: Лань, 2007. — Задача 85.21

