2558. Окружность с центром O
касается сторон угла в точках A
и B
. Через произвольную точку M
отрезка AB
, отличную от точек A
и B
, проведена прямая, перпендикулярная прямой OM
и пересекающая стороны угла в точках C
и D
. Докажите, что MC=MD
.
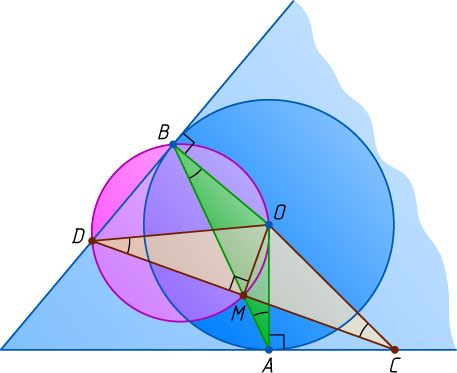
Решение. Рассмотрим случай, изображённый на рисунке. Из точек M
и B
отрезок OD
виден под прямым углом, значит, эти точки лежат на окружности с диаметром OD
. Вписанные в эту окружность углы MDO
и MBO
опираются на одну и ту же дугу, поэтому \angle MDO=\angle MBO
. Аналогично, \angle MCO=\angle MAO
, значит,
\angle CDO=\angle MDO=\angle MBO=\angle ABO=
=\angle BAO=\angle MAO=\angle MCO=\angle DCO,
поэтому треугольник COD
— равнобедренный, его высота OM
является медианой. Следовательно, MC=MD
.
