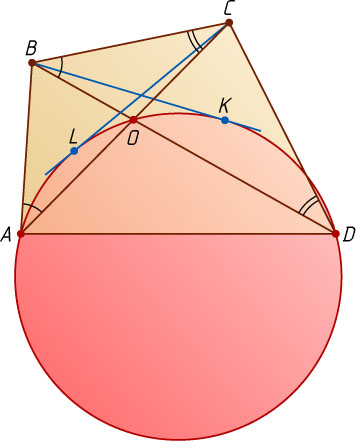
2559. В выпуклом четырёхугольнике ABCD
, диагонали которого пересекаются в точке O
, равны между собой углы BAC
и CBD
, а также углы BCA
и CDB
. Докажите, что касательные, проведённые из точек B
и C
к описанной окружности треугольника AOD
, равны.
Решение. Треугольник ABC
подобен треугольнику BOC
по двум углам, поэтому \frac{CA}{BC}=\frac{BC}{CO}
, откуда CA\cdot CO=BC^{2}
. Аналогично, BO\cdot BD=BC^{2}
, значит, CA\cdot CO=BO\cdot BD
.
Пусть прямая, проведённая через точку B
касается описанной окружности в точке K
, а прямая, проведённая через точку C
, касается этой окружности в точке L
. По теореме о касательной и секущей, BK^{2}=BO\cdot BD
и CL^{2}=CA\cdot CO
, а так как BO\cdot BD=CA\cdot CO
, то BK^{2}=CL^{2}
. Следовательно, BK=CL
.
Источник: Санкт-Петербургская (Ленинградская) математическая олимпиада. — 1985, 9 кл.
Источник: Петербургские математические олимпиады 1961—1993 / Под ред. Д. В. Фомина, К. П. Кохася. — СПб.—М.—Краснодар: Лань, 2007. — Задача 85.25
