2560. Длины сторон выпуклого четырёхугольника не больше 7. Докажите, что четыре круга с радиусами 5 и центрами в вершинах четырёхугольника полностью покрывают четырёхугольник.
Решение. Пусть O
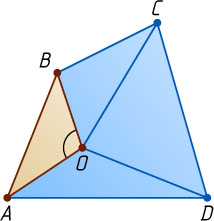
— произвольная точка внутри выпуклого четырёхугольника ABCD
. Тогда хотя бы один из углов AOB
, BOC
, COD
и AOD
не меньше 90^{\circ}
. Предположим, что это угол AOB
. Тогда
OA^{2}+OB^{2}\leqslant AB^{2}\leqslant7^{2}=49,
значит, либо OA^{2}\lt25
, либо OB^{2}\lt25
. Следовательно, точка O
лежит либо внутри круга радиуса 5 с центром A
, либо внутри круга того же радиуса с центром B
.
Источник: Санкт-Петербургская (Ленинградская) математическая олимпиада. — 1985, 9 кл.
Источник: Петербургские математические олимпиады 1961—1993 / Под ред. Д. В. Фомина, К. П. Кохася. — СПб.—М.—Краснодар: Лань, 2007. — Задача 85.27
