2561. Периметр треугольника равен 100 см, а площадь равна 100 см^{2}
. Три прямые, проведённые параллельно сторонам треугольника на расстоянии 1 см от них, разбивают треугольник на семь частей, три из которых — параллелограммы. Докажите, что сумма площадей параллелограммов меньше 25 см^{2}
.
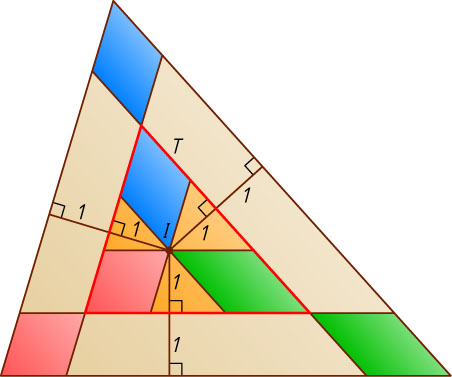
Решение. Пусть T
— треугольник, вершины которого — точки пересечения проведённых прямых, I
— центр окружности радиуса r
, вписанной в данный треугольник, S
— площадь данного треугольника, p
— его полупериметр. Тогда r=\frac{S}{p}=\frac{100}{50}=2
.
Расстояния от точки I
до проведённых прямых равно 1 см, поэтому при гомотетии с центром I
и коэффициентом \frac{1}{2}
данный треугольник перейдёт в треугольник T
, значит, площадь треугольника T
равна четверти площади данного треугольника, так как 25 см^{2}
.
Через точку I
проведём прямые, параллельные сторонам данного треугольника. Они разобьют треугольник T
на три треугольника и три параллелограмма. Суммарная площадь параллелограммов меньше площади треугольника T
, т. е. меньше 25 см^{2}
. Осталось заметить что эти параллелограммы соответственно равны параллелограммам, о которых говорится в условии задачи (если углы одного параллелограмма соответственно равны углам второго и две высоты одного из них соответственно равны двум высотам второго, то параллелограммы равны).
