2562. Трапеция с основаниями a
и b
описана около окружности радиуса R
. Докажите, что ab\geqslant4R^{2}
.
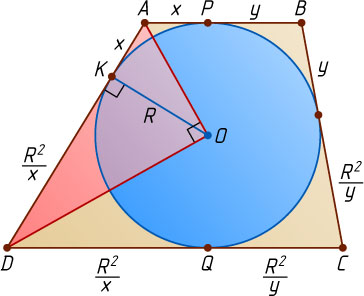
Решение. Пусть окружность с центром O
касается оснований AB
и CD
трапеции ABCD
в точках P
и Q
соответственно, а боковой стороны AD
— в точке K
. Обозначим AP=x
, BP=y
. Тогда x+y=a
.
Лучи AO
и DO
— биссектрисы внутренних односторонних углов BAD
и ADC
при параллельных прямых AB
и CD
и секущей AD
, поэтому \angle AOD=90^{\circ}
. Радиус OK
— высота прямоугольного треугольника AOD
, проведённая из вершины прямого угла, поэтому OK^{2}=DK\cdot AK
, значит,
DQ=DK=\frac{OK^{2}}{AK}=\frac{OK^{2}}{AP}=\frac{R^{2}}{x}.
Аналогично, CQ=\frac{R^{2}}{y}
, поэтому
b=CD=DQ+CQ=\frac{R^{2}}{x}+\frac{R^{2}}{y}=R^{2}\left(\frac{1}{x}+\frac{1}{y}\right).
Следовательно,
ab=(x+y)\cdot R^{2}\left(\frac{1}{x}+\frac{1}{y}\right)=R^{2}\left(\frac{x}{y}+\frac{y}{x}+2\right)\geqslant R^{2}(2+2)=4R^{2}.
Что и требовалось доказать (здесь мы воспользовались известным неравенством \frac{x}{y}+\frac{y}{x}\geqslant2
).
Автор: Генкин С. А.
Источник: Санкт-Петербургская (Ленинградская) математическая олимпиада. — 1985, заключительный тур, 8 кл.
Источник: Петербургские математические олимпиады 1961—1993 / Под ред. Д. В. Фомина, К. П. Кохася. — СПб.—М.—Краснодар: Лань, 2007. — Задача 85.41
Источник: Готман Э. Г., Скопец З. А. Решение геометрических задач аналитическим методом: Пособие для учащихся 9—10 кл. — М.: Просвещение, 1979. — № 260, с. 40
