2563. На сторонах BC
и CD
квадрата ABCD
взяты точки K
и H
соответственно, причём KC=2KB
и HC=HD
. Докажите равенство углов AKB
и AKH
.
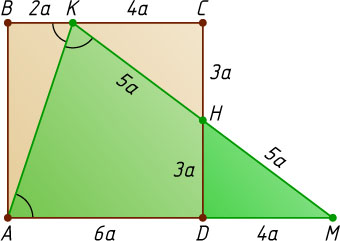
Решение. Пусть сторона квадрата равна 6a
. Тогда KB=2a
, KC=4a
, HC=HD=3a
.
Из прямоугольного треугольника KCH
по теореме Пифагора находим, что
KH=\sqrt{KC^{2}+HC^{2}}=\sqrt{16a^{2}+9a^{2}}=5a.
Продолжим отрезки KH
и AD
до пересечения в точке M
. Прямоугольные треугольники KCH
и MDH
равны по катету и прилежащему острому углу, поэтому MH=KH=5a
и DM=KC=4a
, значит,
KM=KH+MH=10a,~AM=AD+DM=6a+4a=10a.
Треугольник AMK
— равнобедренный, следовательно,
\angle AKH=\angle AKM=\angle KAM=\angle AKB,
что и требовалось доказать.
Источник: Санкт-Петербургская (Ленинградская) математическая олимпиада. — 1986, 7 кл.
Источник: Петербургские математические олимпиады 1961—1993 / Под ред. Д. В. Фомина, К. П. Кохася. — СПб.—М.—Краснодар: Лань, 2007. — Задача 86.18