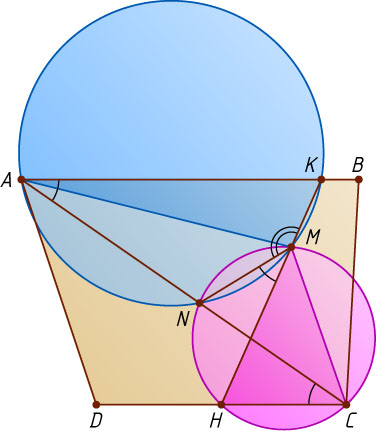
2564. На стороне AB
квадрата ABCD
выбрана точка K
, на стороне CD
— точка H
, и на отрезке KH
— точка M
. Докажите, что вторая (отличная от M
) точка пересечения окружностей, описанных вокруг треугольников AKM
и MHC
, лежит на диагонали AC
.
Решение. Докажем утверждение задачи для любого четырёхугольника ABCD
, у которого AB\parallel CD
.
Пусть N
— отличная от M
точка пересечения указанных окружностей. Вписанные углы NCH
и NMH
опираются на одну и ту же дугу, поэтому они равны. Четырёхугольник AKMN
вписан в окружность, значит, сумма его противоположных углов KAN
и KMN
равна 180^{\circ}
. Таким образом,
\angle NCH=\angle NMH=180^{\circ}-\angle KMN=\angle KAN,
а так как AB\parallel CD
, то точки A
, N
и C
лежат на одной прямой. Отсюда следует утверждение задачи.
Источник: Санкт-Петербургская (Ленинградская) математическая олимпиада. — 1986, 8 кл.
Источник: Петербургские математические олимпиады 1961—1993 / Под ред. Д. В. Фомина, К. П. Кохася. — СПб.—М.—Краснодар: Лань, 2007. — Задача 86.41
