2565. В параллелограмме ABCD
, не являющемся ромбом, проведена биссектриса угла BAD
; X
и Y
— точки её пересечения с прямыми BC
и CD
соответственно. Докажите, что центр окружности, проведённой через точки C
, X
и Y
, лежит на окружности, проведённой через точки B
, C
и D
.
Решение. Обозначим \angle BAD=\angle BCD=\alpha
. Поскольку \angle AXB=\angle DAX=\angle BAX
, треугольники ABX
и XCY
— равнобедренные, поэтому BX=AB
и \angle CXY=\angle CYX=\frac{\alpha}{2}
.
Пусть O
— центр окружности, проходящей через точки C
, X
и Y
. Тогда центральные углы COX
и COY
вдвое больше соответствующих им вписанных углов CYX
и CXY
, т. е. равны \alpha
.
При повороте на угол \alpha
вокруг точки O
, переводящем точку Y
в точку C
, точка C
переходит в X
, отрезок CY
— в отрезок CX
, прямая YD
— в прямую CB
, а так как YD=YC+CD=YC+AB=CX+XB=BC
, то точка D
переходит в точку B
, значит, \angle DOB=\alpha=\angle BCD
.
Из точек O
и C
, лежащих по одну сторону от прямой BD
, отрезок BD
виден под одним и тем же углом, следовательно, эти точки лежат на одной окружности. Отсюда следует утверждение задачи.
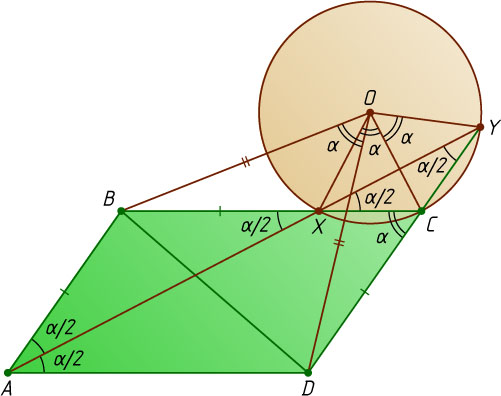
Источник: Санкт-Петербургская (Ленинградская) математическая олимпиада. — 1986, 10 кл.
Источник: Петербургские математические олимпиады 1961—1993 / Под ред. Д. В. Фомина, К. П. Кохася. — СПб.—М.—Краснодар: Лань, 2007. — Задача 86.57
