2585. Диагонали выпуклого четырёхугольника ABCD
пересекаются в точке M
. Пусть P
и Q
— центры окружностей, описанных вокруг треугольников ABM
и CDM
. Докажите, что AB+CD\lt4PQ
.
Решение. Пусть P
и Q
— центры описанных окружностей треугольников ABM
и CDM
соответственно, а биссектриса вертикальных углов AMB
пересекает эти окружности в точках соответственно K
и E
. Тогда AK=BK
, а так как четырёхугольник AKBM
вписанный, то сумма его углов при вершинах A
и B
равна 180^{\circ}
, поэтому один из этих углов, например, MAK
, не меньше 90^{\circ}
. Тогда в треугольнике MAK
против этого угла лежит большая сторона KM
, значит, KM\gt AK=BK
. Аналогично, EM\gt EC=ED
, поэтому 2KM\gt2AK=AK+BK\gt AB
и 2EM\gt2EC=EC+ED\gt CD
, значит, 2KE=2(KM+EM)\gt AB+CD
, или KE\gt\frac{1}{2}(AB+CD)
, а так как проекция отрезка PQ
на KE
равна половине KE
, то
PQ\geqslant\frac{1}{2}KE\gt\frac{1}{2}\cdot\frac{1}{2}(AB+CD)=\frac{1}{4}(AB+CD).
Отсюда следует требуемое неравенство.
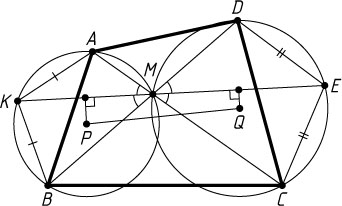
Автор: Назаров Ф. Л.
Источник: Санкт-Петербургская (Ленинградская) математическая олимпиада. — 1991, отборочный тур, 10 кл.
Источник: Журнал «Квант». — 1991, № 11, с. 18, М1314; 1992, № 5, с. 26-27, М1314
Источник: Задачник «Кванта». — М1314
Источник: Журнал «Crux Mathematicorum». — 1996, № 5, задача 6, с. 212
Источник: Петербургские математические олимпиады 1961—1993 / Под ред. Д. В. Фомина, К. П. Кохася. — СПб.—М.—Краснодар: Лань, 2007. — Задача 91.48
