2587. AB
— хорда окружности, делящая её на два сегмента. M
и N
— середины дуг, на которые делят окружность точки A
и B
. При повороте вокруг точки A
на некоторый угол точка B
переходит в точку B'
, а точка M
— в точку M'
. Докажите, что отрезки, соединяющие середину отрезка BB'
с точками M'
и N
, перпендикулярны.
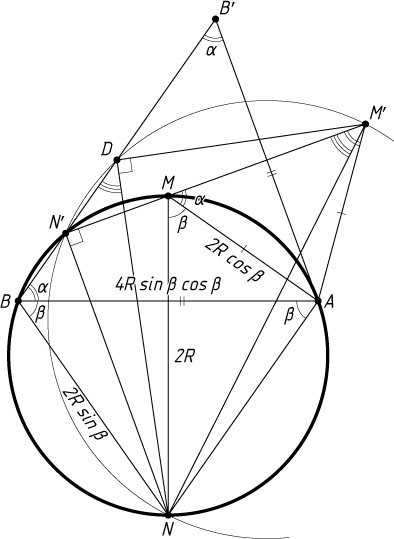
Решение. Обозначим
\angle ABB'=\angle AB'B=\angle AMM'=\angle AM'M=\alpha,
\angle BAN=\angle ABN=\angle AMN=\beta.
Пусть прямые BB'
и MM'
пересекаются в точке N'
. Тогда
\angle AMN'=180^{\circ}-\angle AMM'=180^{\circ}-\alpha=180^{\circ}-\angle ABN',
значит, четырёхугольник AMN'B
вписанный, поэтому точка N'
лежит на данной окружности. При этом MN
— диаметр окружности, значит, \angle NN'M=90^{\circ}
.
Пусть R
— радиус окружности. Тогда
MN=2R,~BN=2R\sin\beta,~AM=2R\cos\beta,
AB=2R\sin(180^{\circ}-2\beta)=2R\sin2\beta=4R\sin\beta\cos\beta,
а так как равнобедренные треугольники AMM'
и ABB'
подобны, то
\frac{MM'}{2BD}=\frac{MM'}{BB'}=\frac{AM}{AB}=\frac{2R\cos\beta}{4R\sin\beta\cos\beta}=\frac{1}{2\sin\beta},
поэтому
\frac{MM'}{BD}=2\cdot\frac{MM'}{2BD}=\frac{1}{\sin\beta}=\frac{MN}{NB}.
Кроме того,
\angle M'MN=\angle AMM'+\angle NMA=\alpha+\beta,~\angle DBN=\angle DBA+\angle NBA=\alpha+\beta,
значит, треугольники M'MN
и DBN
подобны, поэтому \angle NM'N'=\angle NM'M=\angle BDN
. Тогда четырёхугольник DNM'N'
— вписанный, а так как \angle NN'M'=\angle NN'M=90^{\circ}
, то NM'
— диаметр описанной окружности этого четырёхугольника. Следовательно, \angle NDM'=90^{\circ}
. Что и требовалось доказать.
Автор: Насыров З.
Источник: Санкт-Петербургская (Ленинградская) математическая олимпиада. — 1991, отборочный тур, 11 кл.
Источник: Петербургские математические олимпиады 1961—1993 / Под ред. Д. В. Фомина, К. П. Кохася. — СПб.—М.—Краснодар: Лань, 2007. — Задача 91.51
