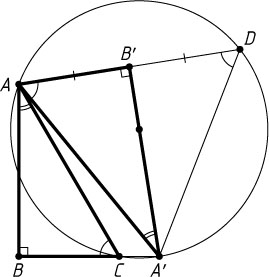
2588. Подобные прямоугольные треугольники ABC
и A'B'A
с прямыми углами при вершинах B
и B'
расположены на плоскости так, что точка A'
лежит на луче BC
за точкой C
. Докажите, что центр окружности, описанной около треугольника A'AC
, лежит на прямой A'B'
.
Решение. Пусть D
— точка, симметричная вершине A
относительно прямой A'B'
. Тогда
\angle ACA'=180^{\circ}-\angle ACB=180^{\circ}-\angle A'AB'=180^{\circ}-\angle ADA',
значит, четырёхугольник ACA'D
— вписанный. Прямая A'B'
— серединный перпендикуляр к хорде AD
, поэтому центр окружности, проходящей через точки A
, A'
и D
, лежит на прямой A'B'
. Осталось заметить, что это описанная окружность четырёхугольника ACA'D
, а значит, и треугольника A'AC
(через три точки, не лежащие на одной прямой, проходит единственная окружность).
Автор: Фомин Д. В.
Источник: Санкт-Петербургская (Ленинградская) математическая олимпиада. — 1992, 9 кл.
Источник: Петербургские математические олимпиады 1961—1993 / Под ред. Д. В. Фомина, К. П. Кохася. — СПб.—М.—Краснодар: Лань, 2007. — Задача 92.24
