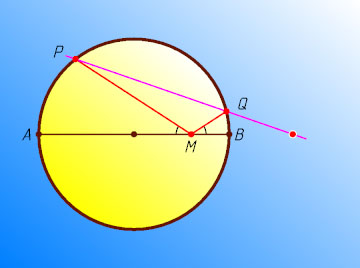
2595. Точка M
находится внутри диаметра AB
окружности и отлична от центра окружности. По одну сторону от этого диаметра на окружности взяты произвольные различные точки P
и Q
, причём отрезки PM
и QM
образуют равные углы с диаметром. Докажите, что все прямые PQ
проходят через одну точку.
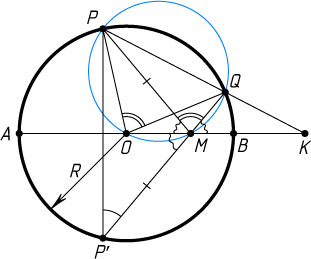
Решение. Продолжим отрезок QM
за точку M
до пересечения с окружностью в точке P'
. Тогда \angle AMP'=\angle QMB=\angle AMP
, значит, при симметрии относительно диаметра AB
, луч MP
переходит в луч MP'
, а так как окружность симметрична относительно любого своего диаметра, то точка P
при этом переходит в P'
.
Пусть O
— центр окружности, R
— её радиус. Угол PMQ
— внешний угол равнобедренного треугольника PMP'
, поэтому
\angle POQ=2\angle PP'Q=2\cdot\frac{1}{2}\angle PMQ=\angle PMQ,
значит, из точек O
и M
, лежащих по одну сторону от прямой PQ
, отрезок PQ
виден под одним и тем же углом. Следовательно, точки P
, Q
, M
и O
лежат на одной окружности.
Пусть прямые PQ
и AB
пересекаются в точке K
. Тогда
KO^{2}-R^{2}=(KO-R)(KO+R)=(KO-OB)(KO+OA)=KB\cdot KA=KQ\cdot KP=KM\cdot KO,
поэтому
KO\cdot OM=KO\cdot(KO-KM)=KO^{2}-KM\cdot KO=R^{2}.
Таким образом, точка K
не зависит от выбора точек P
и Q
. Отсюда следует утверждение задачи.
Автор: Гольберг Е. М.
Источник: Санкт-Петербургская (Ленинградская) математическая олимпиада. — 1993, 10 кл.
Источник: Петербургские математические олимпиады 1961—1993 / Под ред. Д. В. Фомина, К. П. Кохася. — СПб.—М.—Краснодар: Лань, 2007. — Задача 93.32

