2596. Из точки T
провели касательную TA
и секущую, пересекающую окружность в точках B
и C
. Биссектриса угла ATC
пересекает хорды AB
и AC
в точках P
и Q
соответственно. Докажите, что PA=\sqrt{PB\cdot QC}
.
Решение. Из теоремы об угле между касательной и хордой следует, что \angle BAT=\angle ACB=\angle ACT
. По теореме о внешнем угле треугольника
\angle AQP=\angle AQT=\angle ACT+\angle CTQ,
\angle APQ=\angle PAT+\angle ATP=\angle BAT+\angle ATP=\angle ACT+\angle CTQ,
значит, \angle APQ=\angle AQP
, поэтому треугольник APQ
— равнобедренный, AP=AQ
.
По свойству биссектрисы треугольника
\frac{AP}{PB}=\frac{TA}{TB},~\frac{AQ}{QC}=\frac{TA}{TC}.
Перемножив эти равенства, получим, что
\frac{AP\cdot AQ}{PB\cdot QC}=\frac{TA^{2}}{TB\cdot TC}=\frac{TA^{2}}{TA^{2}}=1,
так как TA^{2}=TB\cdot TC
по теореме о касательной и секущей. При этом AP=AQ
, значит, \frac{AP^{2}}{PB\cdot QC}=1
, следовательно, AP=\sqrt{PB\cdot QC}
.
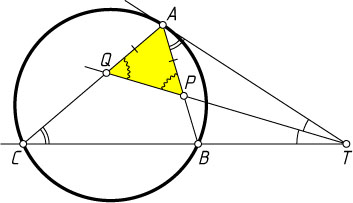
Источник: Всероссийская олимпиада школьников. — 2010-2011, XXXVII, окружной этап, 10 класс
