2597. В треугольнике ABC
угол при вершине B
вдвое больше угла при вершине C
. Окружность с центром в точке A
и радиусом AB
пересекает серединный перпендикуляр к отрезку BC
в точке P
(внутри треугольника). Докажите, что угол PAC
в три раза меньше угла BAC
.
Решение. Обозначим \angle ACB=\alpha
. Тогда \angle ABC=2\alpha
. От луча CA
в полуплоскости, не содержащей точку B
, отложим луч, под углом \alpha
к CA
. Пусть этот луч пересекает серединный перпендикуляр к стороне BC
в точке D
. Тогда треугольник BCD
— равнобедренный, поэтому \angle CBD=\angle BCD=2\alpha=\angle ABC
, значит, точка A
лежит на стороне BD
.
Пусть BE
— биссектриса треугольника BCD
. Треугольник BAE
— равнобедренный, так как AE\parallel BC
и \angle AEB=\angle CBE=\angle ABE=\alpha
, поэтому AE=AB
. Значит, точка E
лежит на окружности с центром A
и радиусом AB
.
Треугольник BDC
симметричен относительно прямой DP
, поэтому
\angle PAC=\angle PEB=\frac{1}{2}\angle PAB
(вписанный угол равен половине соответствующего центрального угла). Следовательно, \angle PAC=\frac{1}{3}\angle BAC
.
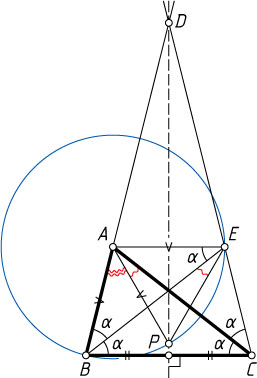
Источник: Всероссийская олимпиада школьников. — 2010-2011, XXXVII, окружной этап, 11 класс
