2605. В прямоугольный треугольник с катетами 6 и 8, вписан квадрат, имеющий с треугольником общий прямой угол. Найдите сторону квадрата.
Ответ. \frac{24}{7}
.
Указание. Рассмотрите подобные треугольники или примените метод площадей.
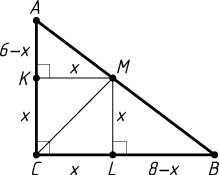
Решение. Первый способ. Пусть вершина M
квадрата CKML
лежит на гипотенузе AB
прямоугольного треугольника ABC
, а вершины K
и L
— на катетах AC
и BC
соответственно; AC=6
, BC=8
. Обозначим сторону квадрата через x
.
Из подобия прямоугольных треугольников ABC
и MBL
следует, что
\frac{BL}{BC}=\frac{LM}{AC},~\mbox{или}~\frac{8-x}{8}=\frac{x}{6},
откуда x=\frac{24}{7}
.
Второй способ. Пусть вершина M
квадрата CKML
лежит на гипотенузе AB
прямоугольного треугольника ABC
, а вершины K
и L
— на катетах AC
и BC
соответственно; AC=6
, BC=8
. Обозначим сторону квадрата через x
. Тогда
S_{\triangle ABC}=S_{\triangle AMC}+S_{\triangle BMC},
\frac{1}{2}AC\cdot BC=\frac{1}{2}AC\cdot MK+\frac{1}{2}BC\cdot ML,
\frac{1}{2}\cdot6\cdot8=\frac{1}{2}\cdot6x+\frac{1}{2}\cdot8x,
откуда x=\frac{24}{7}
.
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 14.5, с. 111
