2627. Теорема о произведениях отрезков пересекающихся хорд. Докажите, что произведения отрезков пересекающихся хорд окружности равны между собой.
Указание. Вписанные углы, опирающиеся на одну дугу, равны между собой.
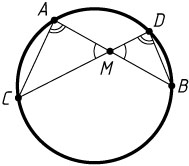
Решение. Пусть хорды AB
и CD
окружности пересекаются в точке M
. Треугольники AMC
и DMB
подобны по двум углам (углы BAC
и BDC
равны как вписанные углы, опирающиеся на одну дугу), поэтому
\frac{AM}{DM}=\frac{CM}{BM}~\Rightarrow~AM\cdot BM=CM\cdot DM.
Источник: Адамар Ж. Элементарная геометрия. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1948. — с. 126-127
Источник: Яглом И. М. Геометрические преобразования. — Т. 2: Линейные и круговые преобразования. — М.: ГИТТЛ, 1956. — с. 222-223
Источник: Калинин А. Ю., Терёшин Д. А. Геометрия. 10—11 классы. — М.: МЦНМО, 2011. — с. 591
