2629. Из точки, расположенной вне окружности на расстоянии \sqrt{7}
от центра, проведена секущая, внутренняя часть которой вдвое меньше внешней и равна радиусу окружности. Найдите радиус окружности.
Ответ. 1.
Указание. Примените теорему о касательной и секущей.
Решение. Пусть секущая, проведённая из точки M
, пересекает окружность с центром O
в точках B
и C
(B
между C
и M
), а прямая MO
пересекает окружность в точках A
и D
(A
между M
и O
). Тогда MB\cdot MC=MA\cdot MD
(оба произведения равны квадрату касательной, проведённой к окружности из точки M
).
Обозначим через r
радиус окружности. Тогда
BC=r,~BM=2r,~MC=3r,~MA=MO-OA=\sqrt{7}-r,~MD=MO+OD=\sqrt{7}+r,
значит, 2r\cdot3r=(\sqrt{7}-r)(\sqrt{7}+r)
. Из этого уравнения находим, что r=1
.
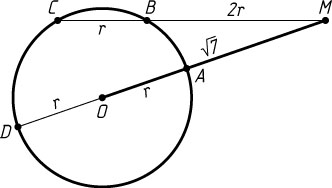
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 12.3, с. 93
